Geometria
DAniel: Na okręgu o promieniu r obrano trzy różne punkty A, B, C tak, że odcinek |AB|=2r oraz
styczna do okręgu w punkcie B i sieczna AC przecinają się w punkcie M. Wiedząc, że styczna do
| | r | |
okręgu w punkcie C przecina odcinek BM w punkcie P takim, że |PM| = |
| oblicz obwód |
| | 2 | |
trójkąta
ABC.
13 lis 08:38
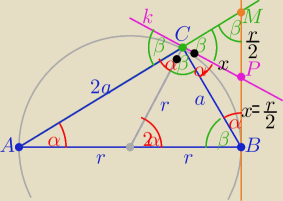
ite: Wstawiam link do rysunku z zaznaczonymi długościami znanych i obliczonych odcinków
oraz ze wszystkimi kątami.
Obliczenia długości boków ΔABC oprzyj na podobieństwie trójkątów ΔABC, ΔBCM, ΔABM
i twierdzeniu Pitagorasa .
Jeśli masz wątpliwości, pytaj.
https://www.geogebra.org/geometry/zezhwssv
13 lis 09:48
moneta:
@
ite 
A co będzie na maturze? Można skorzystać z Geo− Gebry?
1/ rysunek zgodny z treścią zadania
α+β=90
o
|<BCM|=90
o to styczna k połowi odcinek BM⇒ |BM|= r
ΔABC ∼ ΔBMC w skali s= 2r/r=2
|BC|=a ⇒|AC|=2a
Obwód L(ABC)= 2r+3a
z tw. Pitagorasa w ΔABC : 5a
2=4r
2 ⇒ a=.....
L= .......
14 lis 15:42
6latek: Powrót w wielkim stylu .
Mam troche inne zdanie co do uzywania takich programow
14 lis 15:46
ite:
@mon eta z Geo−Gebry nie, ale może da się skorzystać z tego forum? Jeśli matura będzie jak
dotychczas i matematyka będzie /jak dotychczas/.
Ja akurat ćwiczę pieśni, bo ma być więcej pieśni w szkołach.
14 lis 16:56
 @ ite
@ ite  A co będzie na maturze? Można skorzystać z Geo− Gebry?
1/ rysunek zgodny z treścią zadania
α+β=90o
|<BCM|=90o to styczna k połowi odcinek BM⇒ |BM|= r
ΔABC ∼ ΔBMC w skali s= 2r/r=2
|BC|=a ⇒|AC|=2a
Obwód L(ABC)= 2r+3a
z tw. Pitagorasa w ΔABC : 5a2=4r2 ⇒ a=.....
L= .......
A co będzie na maturze? Można skorzystać z Geo− Gebry?
1/ rysunek zgodny z treścią zadania
α+β=90o
|<BCM|=90o to styczna k połowi odcinek BM⇒ |BM|= r
ΔABC ∼ ΔBMC w skali s= 2r/r=2
|BC|=a ⇒|AC|=2a
Obwód L(ABC)= 2r+3a
z tw. Pitagorasa w ΔABC : 5a2=4r2 ⇒ a=.....
L= .......