Funkcje odwrotne Anastazja: Niech g: R −> R będzie zadana następująco: −x² dla x<0 f(x) = (klamra "i") x dla x∊{0,1) 2x−1 dla x ≥ 1 Zbadać czy f jest bijekcją. a jeżeli tak to wyznaczyć f⁻¹ Prosze o pomoc! jutro mam mieć kolokwium na ćwiczeniach z suriekcji i bijekcji a jestem z tego taka głupia

Maciess: Proponuje narysowac sobie wykres tej funkcji i wszystko będzie widac.

chichi: co oznacz zapis x∊{0,1) ?

Maciess: Raczej shift sie wcisnął pani Anastazji przypadkiem

Anastazja: Czyli wszystko wykresem był załatwiła? Bo narysować to łatwo ale skąd wiem czy to bijekcja? i co oznacza f{⁻1}?

chichi: zapis f⁻¹ oznacza funkcję odwrotną

Anastazja: A jaka fukncja odwrotna była by z −x²?

ABC: ja bym pokazywał że pierwsza część klamerki bijektywnie przekształca R⁻ na R⁻ , druga <0,1) na <0,1) a trzecia <1,+∞) na <1,+∞) i ponieważ te zbiory są rozłączne to całość też będzie bijekcją

Anastazja: y = −x² x² = −y x = √−y tak? bo w odpowiedziach jest x = −√−y

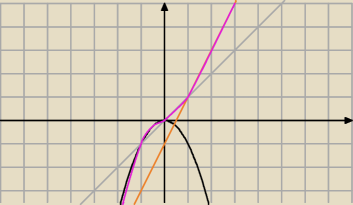
Maciess: No po wykresie zobaczysz czy jest 1−1 i na. Na to znaczy ze przyjmie każdą wartośc z R. A dodatkowo 1−1 to znaczy ze dowolna prosta, rownoległa do osi OX przetnie wykres dokładnie raz. Rozowa funkcja

Anastazja: A wytluamczył byś mi w prostych słowach czym jest 1−1 i na? wiem że to jest suriekcja i injekcja ale nie rozumiem o jest zapisane w "matematycznej definicjii"

Anastazja: BB

Anastazja: Panowie matematycy liczę na pomoc!

ABC: sorry ale to jest tak nudne dla mnie że nie pomogę

Anastazja: Aha dzieki xddddd

Anastazja: No niech Pan taki nie bedzie nooo, tu zależy moa przyszłość od tego

ABC: teraz muszę sprawdzić klasówki z funkcji wymiernych, jak ci za godzinę nikt nie zrobi to pomyślimy

wredulus_pospolitus: iniekcja − czyli gdy funkcja jest różnowartościowa. To znaczy −−− dla każdego 'x' z dziedziny funkcja przyjmuje INNĄ wartość np. f: R −> R ; f(x) = x² nie jest iniekcją (bo chociażby f(−1) = f(1)) ale już f: <0;+∞) −> R ; f(x) = x² jest iniekcją suriekcja −− czyli gdy funkcja jest 'na'. To znaczy −−− funkcja przyjmuje wartości wszystkie wartości z przeciwdziedziny. Albo jak wolisz −−− zbiór wartości funkcji = przeciwdziedzina tejże funkcji. np. f: R −> R ; f(x) = x² nie jest suriekcją (bo chociażby f(x) = −1 nigdy nie zachodzi) ale już f: R −> <0;+∞) ; f(x) = x² jest suriekcją

Anastazja: A miała bym pytanie, jak interpretujesz przeciwdziedzinę?

wredulus_pospolitus: przeciwdziedzina −−− to jest to: f: R −> R <−−− ten drugi zbiór to być przeciwdziedzina

Anastazja: A co w przypadku ja mam f: R −> R²?