czworokąt tom3: W czworokącie wypukłym ABCD kąty przy wierzchołkach A i C są proste AB=m , AD=n i BC=CD Wyznacz długość przekątnej AC

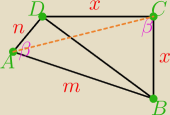
chichi: β=90° Z tw. Pitagorasa w ΔADB: |DB|=√n²+m² Z tw. Pitagorasa w ΔBCD: x=√^n2+m2₂ |∡DAB|+|∡BCD|=2β=180° ⇒ Na czworokącie ABCD można opisać okrąg. Korzystam z tw. Ptolemeusza: |AC|*√n²+m²=√^n2+m2₂*m+√^n2+m2₂*n

	√n2+m2		√n2+m2
|AC|*√n2+m2=		*m+		*n / : √n2+m2
	√2		√2

	√2
|AC|=		(m+n)
	2

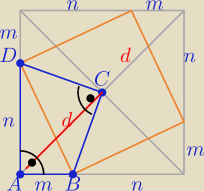Eta: Prawie bez obliczeń

	(m+n)√2
d=
	2

i po ptokach

ABC:

chichi: @Eta świetne rozwiązanie powinnaś zrobić jakiś kurs z rysowania dla forumowiczów haha, porównując nasze rysunki niebo, a ziemia, no cóż

Eta: W zadaniach z geometrii nie znoszę "bohomazów" ! Przejrzysty rysunek ( powtarzam to 10000000 razy) to połowa sukcesu

chichi: Ja się z tym zgadzam w 100%, kwestia tego, że nie potrafię na forum zrobić takiego ładnego rysunku jak na kartce, czy w GeoGebrze. Chodziło mi o rysowanie dokładnie na TYM forum

Eta:

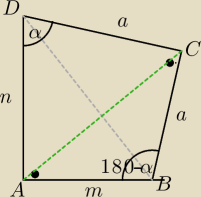a7: jeszcze sposób dla nieznających twierdzenia Ptolemeusza i nie będących olimpijczykami z tw. Pitagorasa dla ΔABD DB=√m²+n²

	n2+m2
z tw Pitagorasa dla ΔBCD 2a2=DB2 ⇒a2=
	2

z tw. cosinusów dla ΔADC i ABC x²=a²+n²−2ancosα i x²=a²+m²−2amcos(180−α) , cos(180−α)=−cosα a²+n²−2ancosα=a²+m²+2amcosα n²−m²=2acosα(m+n) (n−m)(n+m)=2acosα(m+n)

	n−m
cosα=
	2a

	n−m
x2=n2+a2−2an*
	2a

	n2+m2
x2=n2+		−n2+nm
	2

	(n+m)2
x2=
	2

	√2
x=(m+n)*
	2

Eta:

a7: