Rachunek prawdopodobieństwa
Mar12: Z odcinka [0,4] losujemy dwie liczby a i b. Wyznacz prawdopodobieństwo zdarzenia, że a≥1 pod
warunkiem, że a≤b.
11 lis 17:38
wredulus_pospolitus:
| | 1 | | 7 | |
P(a≤1 ∩ a ≤ b) = |
| * |
| |
| | 4 | | 8 | |
11 lis 17:57
Mar12: A mogę prosić o rozpisanie skąd się to bierze?

12 lis 21:47
ABC:
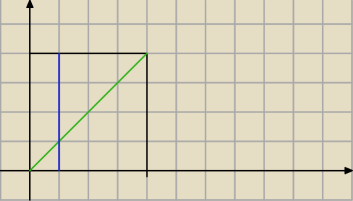
12 lis 22:16
wredulus_pospolitus:
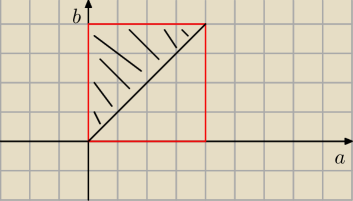
12 lis 22:22
kerajs: | | 15 | |
Moim zdaniem wynikiem jest |
| |
| | 16 | |
12 lis 22:31
ABC:
| 7.5 | | P(A∩B) | |
| zgodnie ze wzorem P(A|B)= |
| |
| 8 | | P(B) | |
12 lis 22:36
wredulus_pospolitus:
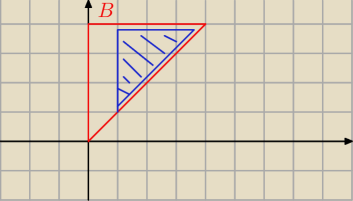
13 lis 00:03
a7:
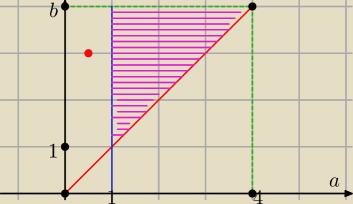
a≥1 jest na i za niebieską linią w prawo P(a≥1)=3/4
a≤b jest na i powyżej prostej a=b (na i nad czerwoną kreską) P(a≥b)=1/2
np. czerwony punkt a=1/2 b=3
| | P(A∩B) | | 4,5 | | 1 | | 9 | |
P(A\B)= |
| P(A∩B)= |
| ={9}{32} P{B}= |
| P(A\B)= |
| |
| | P(B) | | 16 | | 2 | | 16 | |
13 lis 00:59
kerajs: Tak, teraz to poprawne wyniki.
PS
Odpowiedź ABC i moja to prawdopodobieństwo zdarzenia, że a≥1 pod warunkiem, że a≥b.
13 lis 06:29
Mar12: Dziękuuuje bardzo, Wszystko rozumiem

13 lis 08:55




 a≥1 jest na i za niebieską linią w prawo P(a≥1)=3/4
a≤b jest na i powyżej prostej a=b (na i nad czerwoną kreską) P(a≥b)=1/2
np. czerwony punkt a=1/2 b=3
a≥1 jest na i za niebieską linią w prawo P(a≥1)=3/4
a≤b jest na i powyżej prostej a=b (na i nad czerwoną kreską) P(a≥b)=1/2
np. czerwony punkt a=1/2 b=3
