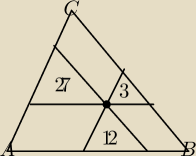
trójkąt surik: Na rysunku pola trójkątów 27,12,3 Oblicz pole ABC

Eta: P(ABC)=108 =======

6latek: Dlaczego tak ? Widze ze jeszcze sa 3 rownolegloboki A co jesli te 3 linie nie bylyby rownolegle do bokow? . dziekuje

Eta: P=(√P₁+√P₂+√P₃)²

6latek: Dziem dobry . Dobrze . Zobacze pozniej do zbioru .

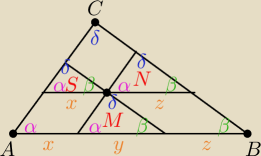
chichi: @Eta pozwól, że uzupełnię twoją wypowiedź z 12:55 o ten krótki dowodzik, ściśle związany z zadaniem i tym co napisałaś . P.S. Dowód oczywiście jest dla ciekawskich i jest banalny Przez punkt położony wewnątrz trójkąta ABC poprowadzono proste równoległe do boków trójkąta ABC. Proste te dzielą trójkąt na sześć części, z których trzy są trójkątami o polach S,M i N. Wykaż, że pole trójkąta ABC jest równe P_ABC=S+M+N+2√SM+2√SN+2√MN.

Eta: @chichi Pozwól,że dokończę i ..... mamy ładniejszy wzorek P_ABC = (√S+√N+√M)²

chichi: @Eta Pewnie, że ładniejszy, ja przepisałem polecenie, ale podejrzewam, że specjalnie został ten wzór tak rozpisany, aby nie było takie oczywiste rozwiązanie, dla licealisty rzecz jasna

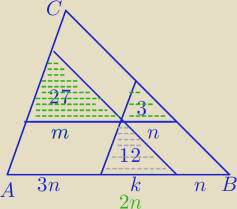
Mila: Z własności: Stosunek pół figur podobnych jest równy kwadratowi skali podobieństwa.

	27		m
1) Δ27∼Δ3⇔		=(		)2
	3		n

m		3
	=		⇔m=3n
n		1

2)

3		n		1		n
	=(		)2 ⇔		=		⇔k=2n
12		k		2		k

3)

	6n
ΔABC∼Δ12 w skali s=		=3
	2n

P_ΔABC=3²*12=9*12=108 Trochę dłużej dla tych, co nie pamiętają wzoru .

chichi: @Mila z tego właśnie korzystałem w dowodzie

chichi:

	x
{		=√SP
	x+y+z

	y
{		=√MP
	x+y+z

	z
{		=√NP
	x+y+z

+ −−−−−−−−−−−−−−−−−−

x+y+z
	=√SP+√MP+√NP
x+y+z

	√S+√M+√N
1=		/ * √P
	√P

√P=√S+√M+√N / ()² P=(√S+√M+√N)²=S+M+N+2√SM+2√SN+2√MN Q.E.D.

Mila: