granica martyna: jak to roziwazac lim_x→0 cos 2x

wredulus_pospolitus: wstaw x=0 i podaj wartość funkcji

martyna: cos0=1 aa czyli to sie stad bierze, nie ma jakiegos wzoru a taka 3^−∞ ? bo na zajeciach napisal, ze 0 a mi sie wydaje ze −∞

martyna: dobra czyli lim_x→0 e^−x = 1 bo jak za x wstawie to kazda liczba do zerowej potegi to, tam mam jeszcze minus ale to moge zrobic odwrotnosc liczby i i tak jak to bedzie do potegi 0 to bedzie 1

martyna: a lim_x→0 ctg x ? skoro ctg0 nie istnieje to jak bedzie, wykres zbliza sie do 0 w +∞

wredulus_pospolitus: martyna ... chwila ... skoro ctg0 nie istnieje (no ok ... nie istnieje) to jak bedzie, wykres zbliza sie do 0 w +∞ ([P[coo ? A co ma piernik do wiatraka? Co ma brak wartości funkcji dla x=0 z wartością funkcji w +∞?]]) Szkoła średnia czy studia

martyna: no jasne ze tak co ma piernik do wiatraka, bo myslalam o tym ze w 0⁺ leci do +∞ studia, ale powtorka ze sredniej

wredulus_pospolitus: tak ... lim_x−>0+ ctg x = +∞

martyna: ale bierzesz to z interpretacji wykresu czy jak mialbys chwile pomoc z reszta przykladow te wyzej, bardzo dziekuje

wredulus_pospolitus:

	cosx		1
limx−>0+ ctgx = limx−>0+		= [		] = +∞
	sinx		0+

wredulus_pospolitus: analogicznie:

	cosx		1
limx−>0− ctgx = limx−>0−		= [		] = −∞
	sinx		0−

martyna: oki, dziekuje bardzo a ktos cos 3^−∞ ile to bedzie −∞? lim_x→0 e^−x to bedzie 1?

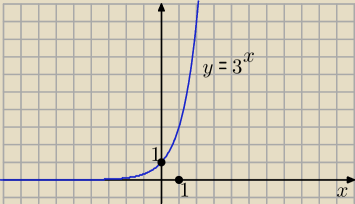
nikt nic: tu łatwo odczytać z wykresu