Iloczyn kartezjański okręgu i przedziału liczbowego w trój-wymiarze Shizzer: Niech K = {(x, y) ∊ R : x² + y² = 1}. Naszkicuj zbiór [−1, 1] x K. 1. Czy ten iloczyn kartezjański będzie wyglądał tak? T = {(x, y, z) ∊ R : x ∊ [−1, 1] ∧ (y, z) ∊ K} 2. Skoro tak to mielibyśmy zbiór wszystkich x'ów z okręgami jednostkowymi o środku w punkcie (y, z) = (0, 0). W zbiorze x'ów [−1, 1] mamy nieskończoną ilość liczb, ponieważ działamy na zbiorze liczb rzeczywistych. Czy prawdą jest, że taki iloczyn kartezjański to nieskończenie wysoki WALEC ze względu na to, że zbiór x'ów jest nieskończony? Bardzo mi zależy na tym, żeby ktoś zweryfikował czy moje rozważania są poprawne. Chciałbym zrozumieć czy dobrze myślę, ponieważ na zajęciach nie budowałem żadnych zbiorów w R³.

Maciess: Przede wszystkim to (x,y,z)∉R tylko do R³

Shizzer: Ok, dziękuję za uwagę, zapamiętam. A czy mógłbym prosić o zweryfikowanie mojego rozważania? Poczułbym się pewniej wiedząc czy wszystko rozumiem czy jednak mam gdzieś błędy

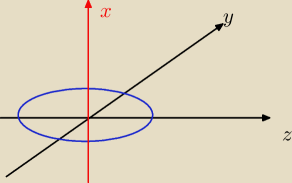
Maciess: Ide sobie po płaszczyźnie. Patrze na dół lezy sobie coś okrągłego. Staje w środku, wygląda mi to na okrąg. Łapie z to moje hulohop i podciągam do siebie na wysokość 1. (nie przechylam). Czemu to ma mieć nieskończoną wysokość?

Shizzer: W układzie współrzędnych ten walec będzie miał dolną podstawę w x = (−3) i górną w x = 4, tak?

ite: Ja tylko zapytam co to jest trój−wymiar? Bo [−1, 1] x K to zbiór par, w których pierwszy element należy do przedziału [−1, 1] (liczby rzeczywiste z tego przedziału?), drugim jest para współrzędnych punktu leżącego na okręgu jednostkowym. ? ?

Shizzer: A jak mogę nazwać układ ze współrzędnymi x, y, z? Myślałem, że mogę napisać trój − wymiar. Jeśli nie to mój błąd

Shizzer: No i wreszcie czy jeśli napisałbym, że powstały walec ma wysokość 7 a nie że jest nieskończenie wysoki to moje rozumowanie byłoby poprawne?

Maciess: Ale skąd ty wziałes sobie te x=−3 i x=4?

Shizzer: Przepraszam. x=−1 i x=1 oczywiście, patrzyłem na inne zadanie stąd mój błąd

Maciess: Ok. ite chodziło pewnie o to, że formalnie taki iloczyn wygląda w ten sposob <x,<y,z>> gdzie x∊R, <y,z>∊R² (czyli na pierwszym miejscu liczba, na drugim para).

Shizzer: Super, wszystko jasne. Bardzo dziękuję za pomoc!