Współrzędne punktów leżących na prostej i okręgu zmartwionyuczeń: rosta 2x−y−5=0 przecina okrąg o środku S(2,4) w punktach A i B. Długość cięciwy AB wynosi 4√5. Znajdź współrzędne punktów A i B.

ICSP: y = 2x − 5 A(x₁ , 2x₁ − 5) B(x₂ , 2x₂ − 5) i niech dodatkowo x₂ > x₁ |AB| = √5|x₂ − x₁| = x₂ − x₁ = 4 ⇒ x₂ = x₁ + 4 A(x₁ , 2x₁ − 5) B(x₁ + 4, 2x₁ + 3) |SA| = |SB| √(x₁ − 2)² + (2x₁ − 9)² = √(x₁ + 2)² + (2x₁ − 1)² x₁ = 2 A(2,−1) B(6,7) lub na odwrót.

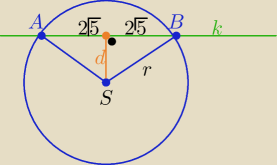
Eta: k: 2x−y−5=0

	|2*2−4−5|
d=		= √5
	√5

r²=(2√5)²+(√5)² = 25 , to r=5 k: y=2x−5 o: (x−2)²+(y−4)²=25 (x−2)²+(2x−9)²=25 ........... x²−8x+12−0 x=2 v x= 6 to y= −1 v y= 7 (2,−1), ( 6,7) −−− współrzędne szukanych punktów A i B ==========

zmartwionyuczeń: Dziękuję!