wektor jaros: Wektor o długości 20 dodano do wektora o długości 25. Długość wektora będącego sumą wektorów może być równa: A) zero B) 3 C) 12 D) 47 E) 50

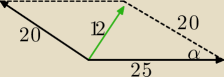
a7: (nie znam się), ale moim zdaniem C) α≈28^o dla długości 3, tw. cosinusów wychodzi sprzeczne cosα>1

kerajs: Długość sumy takich wektorów musi być między 5 (przeciwne zwroty) a 45 (te same zwroty), więc a7 ma rację.

jaros: A mam pytanie @a7 jak do tego doszłaś?

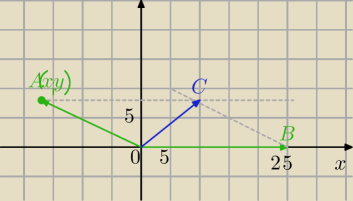
a7: ano sprawdziłam w necie dodawanie wektorów i jest reguła równoległoboku, żeby wektor sumy był krótszy musi być kąt rozwarty między dodawanymi wektorami potem policzyłam długość wektora jak w trójkącie z tw. cosinusów , co nie wiem czy jest na pewno poprawne, dlatego potem znalazłam jeszcze przykładowe wektory dla których C jest spełnione (a B na pewno nie), ale już nie przepisywałam tego ale a powyższym rysunku jeszcze bardziej precyzyjnie (B=(25,0); A=(−17,62;9,5*) *√89,5356 i można policzyć że x²+y²=400 czyli wektor OA=20 wektor OB=25 √(25+x)²+y²=12 625+50x+ x²+y²=144 x=−17,62 y²=89,5356 y≈9,5 i nie jest to sprzeczne natomiast 625+50x+ x²+y²=9 ⇒sprzeczność gdyż wychodzi x=−20,32 to x²+y² byłby większy niż 400 i jest sprzeczność, bo ten wektor ma długość (tylko) 20

a7: tzn. reguła równoległoboku to sprawdź w necie, natomiast "żeby wektor sumy był krótszy..." to był mój wniosek