Czy mi pomożecie to jakoś rozwiązać i zapisać bogusia: Zadanie 3 Rzucono dwiema kośćmi do gry i określono zdarzenia: A − suma wyrzuconych oczek jest większa od 8. B− na obu kościach wypadła ta sama liczba oczek. Oblicz prawdopodobieństwo zdarzenia A∪B.

bogusia: Zadanie 2 W stożek o wysokości długości 5 dm wpisano walec w ten sposób, że dolna podstawa walca zawiera się w dolnej podstawie stożka, a okrąg górnej podstawy walca zawiera sią w powierzchni bocznej stożka. Objętość walca wynosi 16π dm ³, a przekrój osiowy walca jest kwadratem. Oblicz: a) długość wysokości i promienia walca, b) objętość stożka, c) pole powierzchni całkowitej stożka.

bogusia: znalazłam jekies rozwiazanie ale nie wiem czy dobre 2. Ze zbioru liczb {4,5,6,7,...,20} losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo że wylosujemy dwie liczby parzyste. 3. Ze zbioru liczb trzycyfrowych wybieramy jedną liczbę. Oblicz prawdopodobieństwo, że wybierzemy liczbe podzielna przez 120 Ω = {100, 101, 102, ..., 999} Moc zbioru Ω = 900 (moc to dwie poziome kreseczki nad Ω) moc Ω − liczba wszystkich liczb trzycyfrowych A − wylosowanie liczby podzielnej przez 120 A = {120, 240, 360, 480, 600, 720, 840, 960} Moc zbioru A = 8

bogusia: moc zbioru A A P(A) =−−−−−−−−−−−−−−−−−−−− moc zbioru Ω 8 2 P(A) = −−−−− = −−−−− 900 225

bogusia: nie rozumie tylko tego punktu 2 i 3

bogusia: A={(6,3),(6;4),(6;5),(6;6),(5;4),(5;5),(5;6),(4;5),(4;6),(3;6)}=10 Ω=6² B={(6,6),(5;5).....(1;1)}=6 10 6 2 14 P(A∪B)=P(A)+P(B)−P(A∩B)= −−− + −−− − −−−−− = −−− 36 36 36 36

bogusia: Prosze sprawdzić czy dobrze

bogusia: Zadanie 3 Rzucono dwiema kośćmi do gry i określono zdarzenia: A − suma wyrzuconych oczek jest większa od 8. B− na obu kościach wypadła ta sama liczba oczek. Oblicz prawdopodobieństwo zdarzenia A∪B. Rozwiązanie A={(6,3),(6;4),(6;5),(6;6),(5;4),(5;5),(5;6),(4;5),(4;6),(3;6)}=10 Ω=62 B={(6,6),(5;5).....(1;1)}=6 10 6 2 14 P(A∪B)=P(A)+P(B)−P(A∩B)= −−− + −−− − −−−−− = −−− 36 36 36 36

bogusia: Moze ktos sprawdzi i powie ze czy to jest zadanie dobrze rozwiązane

bogusia:

bogusia:

bogusia: Pomożecie

bogusia: Prosze o pomoc i sprawszenie zadania 3

Andrzej: Ω=6² tak, ? tak wynika z dalszych Twoich obliczeń. Dobrze jest.

bogusia: Prosze o pomoc i sprawszenie zadania 3

bogusia: Zadanie 2 W stożek o wysokości długości 5 dm wpisano walec w ten sposób, że dolna podstawa walca zawiera się w dolnej podstawie stożka, a okrąg górnej podstawy walca zawiera sią w powierzchni bocznej stożka. Objętość walca wynosi 16π dm³, a przekrój osiowy walca jest kwadratem. Oblicz: a) długość wysokości i promienia walca, b) objętość stożka, c) pole powierzchni całkowitej stożka.

bogusia: Zadanie 4 Tabela przedstawia pewne dane statystyczne Wartość − 6 −4 6 8 10 12 14 16 Liczebność 45 25 15 15 25 30 20 25 a) Oblicz wariację tych danych b) Wyznacz odchylenie standardowe tych danych z dokładnością do 0,01.

bogusia: Mo = 45 Me = 18:2=9 1130 x = −−−−−−−−−− = 5,65 warjacja 200 ϱ² = 470,6 = √58,825 ale ten wynik nie jest dobry odpowiedz jest inna Bardzo prosze o sprawdzenie

bogusia: w odpowiedzi jest ≈ 8,45 i nie wiem dzie mam błąd

bogusia: ϱ² = √71,3775 ≈ 8,45

bogusia: Pomóżcie!

bogusia: Pomóżcie

bogusia: ?

bogusia: Tabela przedstawia pewne dane statystyczne Wartość − 6 −4 6 8 10 12 14 16 Liczebność 45 25 15 15 25 30 20 25 a) Oblicz wariację tych danych b) Wyznacz odchylenie standardowe tych danych z dokładnością do 0,01. 2 mar 11:02 bogusia: Mo = 45 Me = 18:2=9 1130 x = −−−−−−−−−− = 5,65 warjacja 200 ϱ2 = 470,6 = √58,825 ale ten wynik nie jest dobry odpowiedz jest inna Bardzo prosze o sprawdzenie 2 mar 11:11 bogusia: w odpowiedzi jest ≈ 8,45 i nie wiem dzie mam błąd 2 mar 11:13 bogusia: ϱ2 = √71,3775 ≈ 8,45

bogusia: Nikt mi nie pomoze , ale mam pecha od 3 dni 1 osoba zajrzala

bogusia: ?

bogusia: Pomocy

bogusia:

bogusia: Tabela przedstawia pewne dane statystyczne Wartość − 6 −4 6 8 10 12 14 16 Liczebność 45 25 15 15 25 30 20 25 a) Oblicz wariację tych danych b) Wyznacz odchylenie standardowe tych danych z dokładnością do 0,01. 2 mar 11:02 bogusia: Mo = 45 Me = 18:2=9 1130 x = −−−−−−−−−− = 5,65 warjacja 200 ϱ² = 470,6 = √58,825 ϱ² = 7,69 ale ten wynik nie jest dobry odpowiedz jest inna Bardzo prosze o sprawdzenie 2 mar 11:11 bogusia: w odpowiedzi jest ≈ 8,45 i nie wiem dzie mam błąd 2 mar 11:13 bogusia: ϱ² = √71,3775 ≈ 8,45 POMOZECIE?

bogusia: Rozwiązanie Wariancja n danych liczbowych a1, a2, . . . , an o średniej arytmetycznej a jest liczba (a1 − a)2 + (a2 − a)2 + . . . + (an − a)2 2 =−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− n  – czytamy sigma Odchylenie standardowe  pierwiastek kwadratowy z wariancji  = Mo = 45 Me = 18:2 = 9 x = = = 5,65 2 = = = = = = 470,6 = 7,67 Odp. 2 7,67

Sabin: Po pierwsze, liczymy wariaNcję a nie wariację, bo wariacje to masz w rachunku prawdopodobieństwa. Po drugie, nie przepisuj tego samego posta pod postem bo to się robi szalenie nieczytelne, co to jest Me, co to jest Mo? Średnia policzona OK. Wariancja:

	(−6 − 5,65)2*45 + (−4 − 5,65)2*25 + ... + (16 − 5,65)2*25
σ2 =		= około 71,377
	200

W tym wzorze musisz każdą taką różnicę w nawiasie przemnożyć przez liczebność. stąd odchylenie σ = √σ² = √71,377 = około 8,45

bogusia: Mo to modalne Me to medialne a nie rozumię dlaczego mam pomnożyć przez liczebności

bogusia: Ze wzoru nie wynika ze należy pomnożyc (a1 − a)2 + (a2 − a)2 + . . . + (an − a)2 δ² = −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− n

bogusia: ja odejmowałam i potęgowałam potem dodałam i podzieliłam przez 8

bogusia: Dzięki za podpowiedz i wyszedł prawidłowy wynik

bogusia:

bogusia: Zadanie 2 W stożek o wysokości długości 5 dm wpisano walec w ten sposób, że dolna podstawa walca zawiera się w dolnej podstawie stożka, a okrąg górnej podstawy walca zawiera sią w powierzchni bocznej stożka. Objętość walca wynosi 16π dm 3, a przekrój osiowy walca jest kwadratem. Oblicz: a) długość wysokości i promienia walca, b) objętość stożka, c) pole powierzchni całkowitej stożka

bogusia: moje rozwiązanie Vw =1/3 Πr2 *h = πr2*2r = 2πr3 Vw = 2πr3 = 16π r= ∛8 = 2dm h = 2r = 4dm Vs =1/3 ΠR2 *H L = H − h = 5dm – 4 dm = 1 dm tgα = r/l = R/(H ) R = (r*H)/l = (2*5)/1 = 10dm VStożka = 1/3*Π(10)2*5 = 1/3Π*500 = 500/3Π dm3 S = πR*k k = √(R²+) H² = √(〖10〗²+) 5² = √125 = 25 Sstożka = π*10*25 = 250πdm2 Proszę o sprawdzenie.

bogusia: Pomóżcie mi to jakoś poukladać Z góry dziekuje

bogusia:

bogusia: czerwony, czerwonyPomóżcie mi rozwiązać to zadanie . Bardzo was proszę Zadanie 2 W stożek o wysokości długości 5 dm wpisano walec w ten sposób, że dolna podstawa walca zawiera się w dolnej podstawie stożka, a okrąg górnej podstawy walca zawiera sią w powierzchni bocznej stożka. Objętość walca wynosi 16π dm 3, a przekrój osiowy walca jest kwadratem. Oblicz: a) długość wysokości i promienia walca, b) objętość stożka, c) pole powierzchni całkowitej stożka

bogusia: /

bogusia: czerwony, czerwonyPomóżcie mi rozwiązać to zadanie . Bardzo was proszę Zadanie 2 W stożek o wysokości długości 5 dm wpisano walec w ten sposób, że dolna podstawa walca zawiera się w dolnej podstawie stożka, a okrąg górnej podstawy walca zawiera sią w powierzchni bocznej stożka. Objętość walca wynosi 16π dm³, a przekrój osiowy walca jest kwadratem. Oblicz: a) długość wysokości i promienia walca, b) objętość stożka, c) pole powierzchni całkowitej stożka

bogusia: Pomożecie

bogusia: czerwony, czerwonyPomóżcie mi rozwiązać to zadanie . Bardzo was proszę Zadanie 2 W stożek o wysokości długości 5 dm wpisano walec w ten sposób, że dolna podstawa walca zawiera się w dolnej podstawie stożka, a okrąg górnej podstawy walca zawiera sią w powierzchni bocznej stożka. Objętość walca wynosi 16π dm³, a przekrój osiowy walca jest kwadratem. Oblicz: a) długość wysokości i promienia walca, b) objętość stożka, c) pole powierzchni całkowitej stożka

bogusia: czerwony, czerwonyPomóżcie mi rozwiązać to zadanie . Bardzo was proszę Zadanie 2 W stożek o wysokości długości 5 dm wpisano walec w ten sposób, że dolna podstawa walca zawiera się w dolnej podstawie stożka, a okrąg górnej podstawy walca zawiera sią w powierzchni bocznej stożka. Objętość walca wynosi 16π dm³, a przekrój osiowy walca jest kwadratem. Oblicz: a) długość wysokości i promienia walca, b) objętość stożka, c) pole powierzchni całkowitej stożka

bogusia: pomozecie czekam od poniedzialku ze ktos mi pomoze

bogusia: moze ktos sie zlituje na de mna

bogusia:

bogusia: ?

bogusia:

bogusia: Zadanie 2 W stożek o wysokości długości 5 dm wpisano walec w ten sposób, że dolna podstawa walca zawiera się w dolnej podstawie stożka, a okrąg górnej podstawy walca zawiera sią w powierzchni bocznej stożka. Objętość walca wynosi 16π dm3, a przekrój osiowy walca jest kwadratem. Oblicz: a) długość wysokości i promienia walca, b) objętość stożka, c) pole powierzchni całkowitej stożka Widze ze nikt mi nie umie pomóc

bogusia:

bogusia: Moze ktos da lina na testy z matematyki 2010 oczywiście próbnej

bogusia: ?/

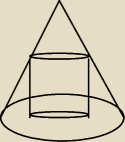
mi: skoro przekrój walca jest kwadratem to wysokość walca= średnicy podstawy walca zatem z objętości walca otrzymujesz V=πr²*H 16π=πr²*2r 8=r³ r=2 zatem H=2r=4

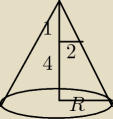
mi: masz dwa trójkąty prostokątne, które są podobne układasz więc proporcję

1		2
	=
5		R

R=10

	1
Vstożka=		πR2*h
	3

	1
Vstożka=		π102*5
	3

	500
Vstożka=		π
	3

mi: do powierzchni całkowietej brakuje ci tylko tworzącej stożka, a to wyliczysz z tw. Pitagorasa 5²+10²=l² 25+100=l² 125=l² l=5√5

mi: Pc=π*10²+π*10*5√5 Pc=100π+50√5π

bogusia: piękne dzięki Jestes wielki albo wielka

Anulka: Mąka i cukier powinny być zmieszane w proporcji 5:3. Ile cukru powinno sie zmieszać z 2 szklankami mąki?

next: 1.2 szklanki