płaszczyzny- geometria analityczna
m: Napisz równanie płaszczyzny przechodzącej przez punkt P(−2,1,2) i równoległej do wektorów:
v=[−1,3,1] i u=[2,−1,0]
Utworzyłam wektor prostopadły do nich
[−1,3,1]x[2,−1,0]=[1,−2,−5]
podstawiłam do wzoru na płaszczyznę i podstawiłam współrzędne punktu:
x−2y−5z+d=0
−2−2−10+d=0
d=14
no i ta płaszczyzna wyszła mi: x−2y−5z+14=0
Coś nie wyszło bo w odpowiedziach jest: −x−2y+5z−10=0 i wyliczone x,y i z
O co tu chodzi?
8 lis 10:27
Blee:
Bo masz źle wyliczony iloczyn wektorowy.
8 lis 10:37
jc:
x=−2−s+2t
y=1+3s−t
z=2+s
8 lis 11:06
m: hm... Liczę iloczyn wektorowy z Sarrusa i wychodzi, a z Laplace'a coś nie wychodzi ta druga
współrzędna:
skreślam drugą kolumnę i wychodzi
|−1 1|
|2 0|
no i mi wychodzi −2
zapętliłam się i nie widzę błędu. Co jest źle?
Rzeczywiście jak wyliczę dobrze iloczyn wektorowy, to wychodzi dobra płaszczyzna
Jak się liczy te x,y,z płaszczyzny i skąd się biorą te s i t?
8 lis 11:21
wredulus_pospolitus:
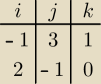
v x u = i(3*0 − 1*(−1)) + j(1*2 − (−1)*0) + k((−1)*(−1) − 3*2) = 1*i + 2*j − 5*k = {1,2,−5]
8 lis 11:33
wredulus_pospolitus:
bo jak skreślasz to mnożysz przez (−1)
jakiej tutaj potęgi 
8 lis 11:34
m: Aa zapomniałam o minusie przy skreślaniu, dzięki. Już wszystko jasne

8 lis 11:37
jc: m:
Mamy równanie parametryczne i równanie ogólne płaszczyzny. s, t to dwa parametry.
Czy autor zadania napisał, w jakiej postaci ma być równanie?
8 lis 11:44
m: to i to, chyba już wiem o co chodzi z tym równaniem parametrycznym
8 lis 12:00
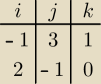 v x u = i(3*0 − 1*(−1)) + j(1*2 − (−1)*0) + k((−1)*(−1) − 3*2) = 1*i + 2*j − 5*k = {1,2,−5]
v x u = i(3*0 − 1*(−1)) + j(1*2 − (−1)*0) + k((−1)*(−1) − 3*2) = 1*i + 2*j − 5*k = {1,2,−5]

