geometria płaska
ktosiu: Przyprostokątne trójkąta prostokątnego ABC mają długość AB=6,4 i AC=4,8. Symetralna boku BC
przecina proste AB i AC w punktach odpowiednio D i E. Oblicz pole trójkąta DBE oraz pole koła
wpisanego w trójkąt DBE
6 lis 22:52
ktosiu:
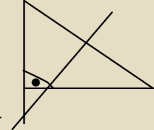
6 lis 22:56
a7:
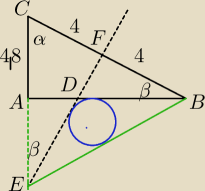
z tw. Pitagorasa BC=8
z podobieństwa trójkątów ABC i CFE (k,k,k)
z tw. Pitagorasa CE=16
√10
AE=4,8−16
√10/3
z podobieństwa trójkątówABC i ADE (k,k,k) AD=3,6−4
√10
DB=AB−AD=6,4−3,6+4
√10=2,8+4
√10
P
BDE=1/2*DB*AE=........
6 lis 23:29
Eta:
|CE|=20/3
6 lis 23:46
chichi: | | 20 | |
@Eta mi też wyszło |CE|= |
| |
| | 3 | |
6 lis 23:53
Eta:
chichichi

6 lis 23:56
a7:
tak, faktycznie
CF
2+EF
2=CE
2
16+256/9=CE
2
CE
2=400/9
CE=20/3
| | 20 | | 24 | | 13 | |
AE=6 |
| −4 |
| =1 |
| |
| | 30 | | 30 | | 15 | |
AD=1,4
DB=6,4−1,4=5
P=.....
r=....
: )
6 lis 23:56
a7: @chichi brawo

6 lis 23:58
Eta:
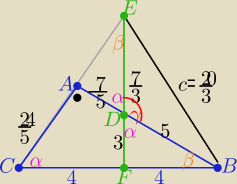
|BC|=8
Z podobieństwa trójkątów ABC i DFB z cechy (kkk)
| BD | | 8 | | 7 | |
| = |
| ⇒ |BD|=5 to |AD|=1,4= |
| |
| 4 | | 6,4 | | 5 | |
i z podobieństwa trójkątów BFD i AED
| | 20 | |
z tw. Pitagorasa w ΔEFB c= |
| |
| | 3 | |
Obwód ΔBDE = 14, p=7
| | 1 | | 7 | | 4 | | 14 | |
P(BDE)= |
| * |
| *5* |
| = |
| |
| | 2 | | 3 | | 5 | | 3 | |
======
7 lis 01:26

 z tw. Pitagorasa BC=8
z podobieństwa trójkątów ABC i CFE (k,k,k)
z tw. Pitagorasa BC=8
z podobieństwa trójkątów ABC i CFE (k,k,k)



 |BC|=8
Z podobieństwa trójkątów ABC i DFB z cechy (kkk)
|BC|=8
Z podobieństwa trójkątów ABC i DFB z cechy (kkk)