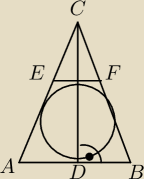 W trójkąt równoramienny ABC wpisano okrąg o promieniu 3 cm. Odcinek EF styczny do tego okręgu
jest równoległy do podstawy AB. Wiedząc, że PABFE = 15 * PEFC oblicz:
a) obwód trójkąta EFC
b) pole trójkąta ABC
c) wysokość CD trójkąta ABC
d) długość podstawy AB.
W trójkąt równoramienny ABC wpisano okrąg o promieniu 3 cm. Odcinek EF styczny do tego okręgu
jest równoległy do podstawy AB. Wiedząc, że PABFE = 15 * PEFC oblicz:
a) obwód trójkąta EFC
b) pole trójkąta ABC
c) wysokość CD trójkąta ABC
d) długość podstawy AB.


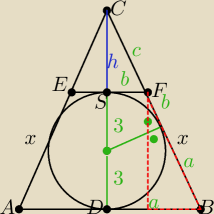
| 2a+2b | ||
(1)PABEF=15*PEFC | *6=15*1/2*2b*h⇒ h=2/5(a+b) | |
| 2 |
| h | b | 54 | ||||
(3) z podobieństwa trójkątow CSF i CDB | = | ⇒ h= | ||||
| h+6 | a | a2−9 |
| a2+9 | 54 | |||
h=2/5 ( | )= | ⇒ a=3√216=6 | ||
| a | a2−9 |
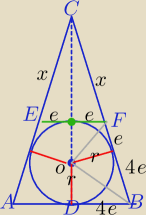 Można tak, ale są inne sposoby.
1) PΔABC=16P
Można tak, ale są inne sposoby.
1) PΔABC=16P
| 1 | 1 | |||
ΔEFC∼ΔABC w skali k= | = | |||
| √16 | 4 |
| 3 | ||
r2=e*4e ⇔9=4e2⇔ e= | ||
| 2 |
| 3 | ||
|AB|=8* | =12 | |
| 2 |
| 1 | ||
|EF|= | *12=3m | |
| 4 |
| x | 1 | 3 | |||
= | ⇔4x=x+5* | ||||
| x+5e | 4 | 2 |
| 5 | ||
x= | cm | |
| 2 |
| 3 | 5 | |||
4) obwΔEFC=2* | +2* | =8cm | ||
| 2 | 2 |
| 32 | ||
PΔABC=p*r= | *3 | |
| 2 |
| 1 | ||
3cm2= | *3*he | |
| 2 |


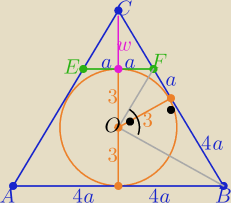 Ja liczyłam tak:
P(ABEF)=15P(EFC) to P(ABC)= 16P(EFC)
Skala podob. ΔABC i EFC : k2=16 ⇒ k=4
to w=2, |CD|=8
W ΔBOF : 4a2=9 ⇒ a=3/2
|AB|=8a= 12 b=|BC|= 10 P(ABC)=48
L(ABC)=32 to L(EFC)= 32/4 =8
Ja liczyłam tak:
P(ABEF)=15P(EFC) to P(ABC)= 16P(EFC)
Skala podob. ΔABC i EFC : k2=16 ⇒ k=4
to w=2, |CD|=8
W ΔBOF : 4a2=9 ⇒ a=3/2
|AB|=8a= 12 b=|BC|= 10 P(ABC)=48
L(ABC)=32 to L(EFC)= 32/4 =8
| a | 3 | ||
= | podobieństwo trójkątów prostokątnych w trójkącie BOF (uzyskanych przez | ||
| 3 | 4a |
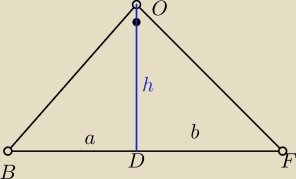 jest taka zależnosc w trojkącie prostokątnym
wysokosc h =|OD|=√|BD|*|DF|
jest srednia geometryczna tych odcinkow
h=√a*b
h2=a*b
tutaj masz h=3 i dlugosci odcinkow na jakie ta wysokosc dzieli podstawe czyli a i 4a
stad masz 9=a*4a=4a2
Pytanie tylko czy wiesz dlaczego ten trojkat BOF jest prostokatny ?
jest taka zależnosc w trojkącie prostokątnym
wysokosc h =|OD|=√|BD|*|DF|
jest srednia geometryczna tych odcinkow
h=√a*b
h2=a*b
tutaj masz h=3 i dlugosci odcinkow na jakie ta wysokosc dzieli podstawe czyli a i 4a
stad masz 9=a*4a=4a2
Pytanie tylko czy wiesz dlaczego ten trojkat BOF jest prostokatny ?
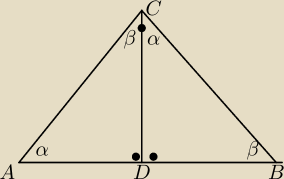 Nr 1
na podstawie cechy K−K−K
Nr 2
Patrz rysunek Ety
mamy czworokąt ABFE
Mozna w niego wpisac okrąg
Srodek okregu wpisanego w czworokat lezy na przecieciu sie dwusiecznych kątów
Kąt ABF i kąt EFB to kąty przyległe a dwusieczne kątów przyległych przecinają sie pod kątem
prostym
Stąd kąt FOB jest kątem prostym i ΔFOB jest Δ prostokątnym . Pamiętaj o tym to sie przydaje w
zadaniach
Nr 1
na podstawie cechy K−K−K
Nr 2
Patrz rysunek Ety
mamy czworokąt ABFE
Mozna w niego wpisac okrąg
Srodek okregu wpisanego w czworokat lezy na przecieciu sie dwusiecznych kątów
Kąt ABF i kąt EFB to kąty przyległe a dwusieczne kątów przyległych przecinają sie pod kątem
prostym
Stąd kąt FOB jest kątem prostym i ΔFOB jest Δ prostokątnym . Pamiętaj o tym to sie przydaje w
zadaniach