graniastosłup Dominik: Dany jest graniastosłup prawidłowy trójkątny ABCDEF o podstawach ABC i DEF Okrąg wpisany w podstawę ma długość r Punkty P i Q są odpowiednio środkami odcinków AB i BE, a kąt PCQ ma miarę α Wyznacz objętość tego graniastosłupa Mogę liczyć na pomoc ?

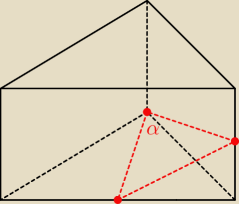
wredulus_pospolitus: 1) zauważ, że trójkąt PCQ jest to trójkąt równoramienny o kącie przy podstawie równym α

	1		√a2 + h2
|PQ| =		|AE| =
	2		2

	√(2a)2 + h2
|CQ| = √a2 + (h/2)2 =
	2

	a√3
|PC| =
	2

2) a = √3r 3) z tw. cosinusów |PQ|² = |CQ|² + |PC|² − 2|CQ|*|PC|*cosα wyznaczasz 'h' podstawiasz do wzoru na objętość

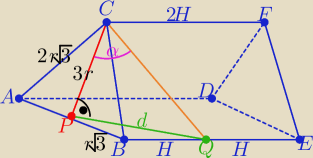
Eta: V= P_p*2H P_p= 3r²√3 W ΔPCQ : d= 3r*tgα W ΔPBQ z tw. Pitagorasa H²=d²−(r√3)² H²= 9r²tg²α−3r² ⇒ H=r√3√3tg²α−1 V= ............ V= 18r³√3tg²α−1 ==============

Eta: @ Wredulus Na jakie podstawie twierdzisz,że ΔPCQ jest równoramienny ?

wredulus_pospolitus: A ... nie wykasowałem tego ... upsik