krata podgrup Krulik: Hej, mam znaleźć kratę podgrup Z₃₆^x. Zaczynam rozpisywać generatory, najpierw 1 elementowe, później 2−elementowe: <1>={1} <3>={1,3,9,11,33,27} <5>={1,5,25,17,13,29} i tak dalej. I tak w jakiejś 1/3 stwierdziłem, że to dużo roboty, bo jak wchodzą już generatory 2 elementowe tzn: <3,7>={1,3,7,21,27,13,9,19,25,31} i tak dalej. Strasznie tego dużo, i co chwilę wychodzą nowe. Jak to zrobić prościej? Jeżeli wgl jest opcja. Pozdrawiam

jc: Z₃₆^*={1,5,7,11,13,17,19,23,25,29,31,35} podgrupy: {1,5,7,11,13,17,19,23,25,29,31,35} {5,25,17,13,29,1} {25,13,1} {17,1} {1}

jc: Generatory podgrup: 7, 5, 13, 17, 1

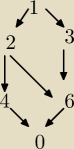
jc: Jeszcze inaczej. g=7, generator grupy. g¹2=e generatory podgrup: g, g², g³, g⁴, g⁶, e

Krulik: To naprawdę są wszystkie podgrupy? Coś mi nie pasuje albo czegoś nie rozumiem, co w takim razie np. z podgrupą generowaną przez <9>={1,9}?

jc: Z_n^* to grupa elementów odwracalnych z mnożeniem. 9 nie jest elementem odwracalnym.

Słoniątko: 9 nie jest odwracalne w Z₃₆

Krulik: Oooo, dobra rozumiem, korzystałem z przykładu Z₁₆^x i tam podgrupami były wszystkie generowane przez generatory za wyjątkiem tych które się powtarzają. A tutaj dostaniemy wiele zbiorów które się nie powtarzają, ale ich elementy nie mają odwracalnych w danym zbiorze. Możecie mi jeszcze wytłumaczyć tą grafikę?

jc: Oj pomyliłem się, to nie jest grupa cykliczna. {7, 13,19,25,31,1} {5,25,17,13,29,1} {11,13,35,25,23,1} {13,25,1} {17,1} {19,1} {35,1} Teraz rysuj diagram.

Słoniątko: grafika pokazuje ci jakimi drogami idziesz od g −oznaczone jako 1 do g¹²=e , który to element przedmówca oznaczył 0

Krulik: Kompletnie nie rozumiem jak to tak szybko znalazłeś

jc: {1,5,7,11,13,17,19,23,25,29,31,35} {7, 13,19,25,31,1} {5,25,17,13,29,1} {11,13,35,25,23,1} {13,25,1} {17,1} {19,1} {35,1} {1} Mamy też podgrupy niecykliczne? {17,19,35,1} Czy coś jeszcze?

jc: Czy to nie jest C₆ x C₂?

Krulik: Dobra, zrozumiałem, ten zapis g do potęgi mnie zmylił.

Krulik: tzn chyba zrozumiałem, zaraz sprawdzę na innym przykładzie

jc: a²=e=b⁶, ab=ba 1: <e> 2: <a>, <b³>, <ab³> 3: <b²>, 4: <b³, a> 6: <b>, <ab>, <a, b²> 12 <b, a>

jc: Krulik, pisząc g myślałem, że to grupa cykliczna. To nie jest grupa cykliczna!

jc: To grupa trylinki (symetria względem płaszczyzny poziomej i obroty wokół pionowej osi).

Krulik: w takim razie znów nie rozumiem jak w tak krótkim czasie doszedłeś do tych właściwych podgrup

Krulik: tym bardziej, że ten sposób powyżej sprawdza się w większości przypadków dla grup z dodawaniem z tego co widzę, dla mnożenia ciężko

Krulik: tzn sposób z grafiką który ogarniałem w tym czasie

jc: Oj, nie tak szybko. 20 minut + pomoc komputera (liczenie kolejnych potęg) + dwie kartki rysunków. Do tego kilka wcześniejszych błędów.

Krulik: ale skoro zbiory generowane przez pojedyńczy element nie dały całego Z₃₆^x, to wtedy musimy sprawdzać generatory 2 elementowe, a nawet i 3 elementowe w sumie, przecież tego jest ogromnie dużo, samych zbiorów generowanych przez 2 elementowe jest 11*10:2=55 bo jedynki nie trzeba liczyć. Musi być jakiś prostszy sposób niż ten którym robiłem ja. A i jeszcze jedna sprawa, W Z₃₆^x są tylko liczby względnie pierwsze z 36? Bo ja tam dorzuciłem jeszcze trójki, dziewiątki a widzę że ty ich nie masz.

Krulik: Dobra, faktycznie łatwe, po prostu dorzuciłem trójki do tego i zaczęły mi wychodzić dziwne wyniki

Krulik: Dzięki.