Różne Jeszcze student: Obliczyć: 1. x^{log5 36} − 13*6^{log5 x} +42 = 0 2. log(log(x)) + log(x²−1) = 1 3. arcsinx + arcsin2x = π/2

wredulus_pospolitus: 1) do rozwiązania będzie potrzebne wykorzystanie własności logarytmów: a^log_bc = c^log_ba jeżeli nie miałeś jej podanej ... musisz ją wykazać (nie jest to trudne)

wredulus_pospolitus: 2) na pewno TAK DOKŁADNIE wygląda to równanie?

Jeszcze student: 2) Słowo w słowo przepisane jest...

Jeszcze student: Dzięki, pierwsze zrobione, nie znałem tej własności, ale jest faktycznie prosta do zrobienia.

wredulus_pospolitus: (2) pytałeś się dlatego, że ... to nie jest łatwe do do rozwiązania ... a raczej, po paru przekształceniach dochodzimy do równania którego po prostu raczej nie będziesz w stanie wyznaczyć chyba że to jest log( logx + log(x²−1) ) = 1

Eta: Wredulus raczej tak: 2/log[logx*(x²−1)]=1

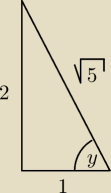
wredulus_pospolitus: 3) tutaj pomocna może się okazać pewna własność:

	π
arcsinx + arccosx =
	2

więc mamy:

	1
arcsin(2x) = arccosx ⇔ cos y =		siny −−> tgy = 2
	2

i teraz budujemy trójkąt prostokątny

	1		1		√5
z którego mamy: cos y =		= x −−−> x =		=
	√5		√5		5

Jeszcze student: 2) Trzecie zadanie tutaj: https://imgur.com/8nKgBiT

wredulus_pospolitus: bez tej własności będzie trochę dłużej, ale też damy radę: arcsinx = z ⇔ siny = x arcsin(2x) = π/2 − z ⇔ sin(π/2 − z) = 2x ⇔ cosz = 2x i stąd mamy:

	1
cosz = 2sinz −−−> tgz =		i znowu budujemy trójkąt, ale uwaga kąt z to nie ten sam kąt
	2

co kąt y (a przy drugiej przyprostokątnej)

wredulus_pospolitus: no to kurdę trochę się różni od tego co napisałeś log(log(x)) + log(log x² −1) = 1

Jeszcze student: Przepraszam, od 10 przy komputerze mi nie sprzyja...

wredulus_pospolitus: Trochę okrężną drogą, ale może będzie Ci łatwiej: 1) log (x²) − 1 = log (x²) − log 10 = log(x²/10) 2) log ( logx) + log(log(x²/10) = log( logx * log(x²/10)) 3) log( logx * log(x²/10)) = 1 log( logx * log(x²/10)) = log 10 logx * log(x²/10)) = 10 logx * [ log (x²) − log 10] = 10 log x * [ 2logx − 1] = 10 t = logx 2t² − t − 10 = 0 −−−> t =

wredulus_pospolitus: A trochę szybciej: log(log(x)) + log( log(x²) −1) = 1 log( logx * [ log(x²) − 1] ) = log 10 logx * [ log(x²) − 1] = 10 logx * [ 2log(x) − 1] = 10 t = logx 2t² − t − 10 = 0

Jeszcze student: Banał, czas się wyspać, bo ślepota łapie. Pozdrawiam Panowie i dzięki. Gdzie Wasz Patronite?

wredulus_pospolitus: Spoko ... zaraz Ci dam link do naszego konta 'only fans' na którym po dokonaniu 'malutkiej' opłaty będziesz miał dostęp do najciekawszych przykładów A tak serio −−− zawsze możesz wysłać smsa który pomoże utrzymać Jakubowi to forum

wredulus_pospolitus: https://matematykaszkolna.pl/premium.html

chichi: @wredulus dzieci też są na tej stronie haha, a ty takie propozycje rzucasz

wredulus_pospolitus: Obawiam się, że dzieciaki lepiej zdają sobie sprawę ze sprawy niż nasi weterani 40+

chichi: To, że wiedzą to pół biedy, gorzej mają się karty kredytowe tatusiów