asymptota ukośna xxx: hej, mam obliczyć asymptotę pionową i ukośną takiej funkcji: ^(x−3)2_2x²−2 nie wiem czy dobrze widać więc napiszę jeszcze jak wyglada ten wzór, licznik to kwadrat roznicy x−3, mianownik to 2 razy x do kwadratu odjąć 2 as. pionową wyliczyłam i jest to x=1 oraz x=−1 gdy liczę as. ukośną y=ax+b, a wychodzi mi 0, zaś b=¹₂, więc wychodziłoby że as. ukośna to y=¹₂ jednak gdy wpisałam wzór tej funkcji do kalkulatora graficznego funkcja wygląda jakby nie miała w ogóle as. ukosnej, a na pewno nie równą ¹₂ byłabym bardzo wdzięczna gdyby mi ktoś pokazał gdzie mam błąd

wredulus_pospolitus:

	(x−3)2
f(x) =
	2x2−2

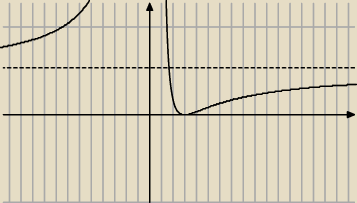
No jak dla mnie to jest y = 0.5 zauważ, że asymptota pozioma jest szczególnym przypadkiem asymptoty ukośnej druga sprawa:

	(x−3)2		x2 − 6x + 9		x2 − 1 −6x + 10
f(x) =		=		=		=
	2x2 − 2		2x2 − 2		2x2 − 2

	1		6x − 10
=		−
	2		2x2 − 2

Z tej postaci łatwo zauważyć, że

	1		1
limx −> ±∞ f(x) =		− 0 =
	2		2

Fretkonur: Jak chcesz żeby ułamki wyglądały lepiej zamiast "u" użyj "U" i nie będzie nigdy więcej problemu

wredulus_pospolitus: Taka uwaga jako że asymptota pozioma jest szczególnym przypadkiem asymptoty ukośnej (a szybciej się ją liczy), to lepiej zacząć od liczenia asymptoty poziomej czyli lim_{x −> ±∞} f(x) i dopiero gdy

	f(x)
tej granicy nie ma to policzyć limx −> ±∞
	x

xxx: wredulus pospolitus dziękuję za pomoc! myślałam, że gdy jest asymptota to nie moze być na niej żaden punkt tak jak jest w tym przypadku (że asymptota nie może przecinać wykresu) dlatego też myslałam że to jest źle a to mam tez pytanie odnosnie Twojej drugiej wypowiedzi, czyli gdy wyjdzie mi asymptota pozioma to ukosnej nie muszę już liczyc, bo wtedy ta pozioma jest tym szczególnym przypadkiem ikosnej tak? a jednoczesnie asymptoty poziomej i ukosnej, że dwóch na raz nie ma, tak? Fretkonur dzięki! na pewno to wykorzystam

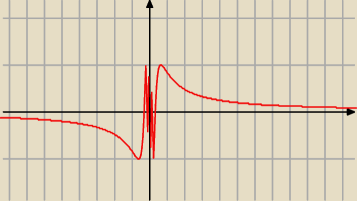
wredulus_pospolitus: przeważnie mamy tak, że asymptota jest 'nie przecinana' przez wykres funkcji gdzieś 'daleko w ±∞' ... bliżej okolic x=0 czasem się zdarza, że przetnie się wykres funkcji z asymptotą, ale to nie wpływa na nic. Jednak spójrz sobie na funkcję f(x) = sin(1/x) ... funkcja ta posiada asymptotę poziomą y = 0, a przecież ta funkcja NIESKOŃCZENIE WIELE RAZY przecina asymptotę dla 'małych 'x' ' ale później już spokojnie dąży wykres funkcji do y = 0 Tak ... jeżeli jest pozioma, to już nie ma co liczyć ukośnej, bo ta pozioma jest ukośną Pamiętaj jednak, że może się trafić taka funkcja, że będzie miała INNĄ asymptotę w −∞, a inną w +∞

xxx: okej, dziekuję bardzo za wszystkie wyjasnienia, teraz juz wszystko rozumiem