indukcja matematyczna Chorus: Wykaż następującą relację: 1+3+5+ ... (2n−1) = n²

ICSP: 1 + 3 + 5 + ... + (2n−1) = S (2n−1) + (2n − 3) + ... + 1 = S −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− [1 + 2n−1] + [3 + 2n − 3] + ........... + [2n − 1 + 1] = S + S 2n + 2n + .... + 2n = 2S n(2n) = 2S S = n²

Chorus: chciałbym wiedzieć skąd się bierze (2n−1) + (2n − 3) + ... + 1 = S próbowałem podstawić za n= k+1 ale trochę się pogubiłem

wredulus_pospolitus: Bo to jest zapisana pierwsza równość w odwrotnej kolejności 1 + 3 + 5 .... + (2n−5) + (2n−3) + (2n−1) = S (2n−1) + (2n−3) + (2n−5) +.... + 5 + 3 + 1 = S

Mariusz: No fajnie tyle że miał to pokazać z indukcji matematycznej A jeśli chodzi o samo wyprowadzenie wzoru to proponuję rachunek różnicowy Zdaje się że na ważniaku coś o tym mają

znak: 1 + 3 + 5 + .. + (2n − 1) = n² Dla n = 1: 1 = 1 W takim razie dla n + 1: 1 + 3 + ... + (2n − 1) + (2n + 1) = n² + (2n + 1) = n² + 2n + 1 = (n + 1)² Ta pogrubiona część to skorzystanie z założenia indukcyjnego.

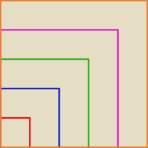
kerajs: Dowód geometryczny