Nierówności kwadratowe Samson: |x²+6x−1|≤6 Witam, mam do rozwiązania tą nierówność, wyniki powinny wyjść: Czy dobrze to zrobiłem? x² + 6x − 1 ≤ 6 x² + 6x − 7 ≤ 0 Δ = 36 + 28 = 64 x1 = (−6−8)/2 = −7 x2 = (−6+8)/2 = 1 i dla drugiego przypadku Δ = 36 − 20 = 16 x3 = (−6−4)/2 x4 = (−6+4)/2 x3 = −5 x4 = −1 Czy niczego nie brakuje? Jak będzie wyglądał wykres, jęsli ktoś może pokazać, bo mam z tym problemy

ICSP: Nie rozumiem drugiego warunku. Jest on podzbiorem pierwszego.

ICSP: |x² − 6x − 1| ≤ 6 ⇒ x² − 6x − 1 ≤ 6 ∧ x² − 6x − 1 ≥ −6

Samson: Wolfram też pokazuje takie rozwiązania

Samson: Zrobiłem tak jak piszesz, raz z 6 a raz z − 6

ICSP: Strasznie to chaotyczne. Ale skoro wynik się zgadza z wolframem to chyba nie ma problemu.

getin: x1, x2, x3, x4 jest okej dokładnego wykresu funkcji nie trzeba rysować aby rozwiązać nierówność rozwiązaniem nierówności x²+6x−1≤6 jest przedział <−7, 1> rozwiązaniem nierówności x²+6x−1≥−6 jest przedział (−∞, −5> u <−1, +∞) rozwiązaniem nierówności |x²+6x−1|≤6 jest część wspólna zbioru <−7, 1> i zbioru (−∞, −5> u <−1, +∞). Czyli będzie to ostatecznie <−7,−5> u <−1, 1> Pytania ?

Samson: x² + 6x − 1 ≤ −6 x² + 6x − 5 ≤ 0 Δ = 36 − 20 = 16 x1 = (−6−4)/2 = −5 x2 = (−6+4)/2 = −1

Samson: Dziękuję getin

ICSP: zły znak nierówności.

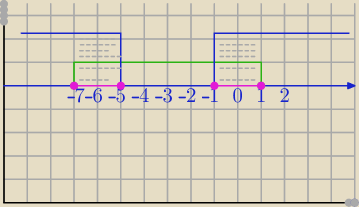
Mila: |x²+6x−1|≤6⇔ −6≤x²+6x−1≤6⇔ x²+6x−5≥0 i x²+6x−7≤0⇔ (x≤−5 lub x≥−1) i −7≤x≤1⇔ x∊<−7,−5>∪<−1,1>

Samson: Dziękuję Mila A nie powinno tam być x² + 6x + 5 , zamiast − 5?

Jerzy: Powinno.

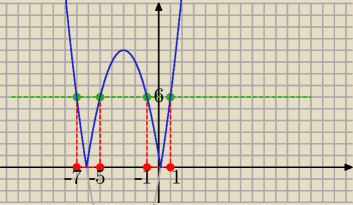
Eta: graficznie: Odp: x∊<−7,−5> U <−1,1>