Zadanie z ciągów Adelajda:

	nπ
Wyznacz granicę dolną i górną ciągu an = 4 * (−1)n + cos
	4

wredulus_pospolitus:

	8kπ
górna: 4(−1)8k + cos		= 4 + 1 = 5
	4

	8kπ + 3π		√2
dolna: 4*(−1)8k + 3 + cos		= −4 −
	4		2

wredulus_pospolitus: n = 8k + 5 także będzie przyjmować wartość 'dolnej granicy'

Adelajda: A gdybym mokła spytać, skąd się wzięło 8k +3?

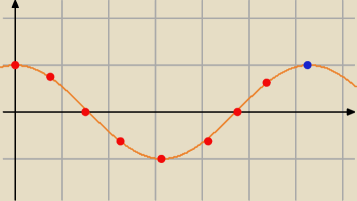
wredulus_pospolitus: mogła* po prostu popatrzyłem sobie na wykres cosinusa i pozaznaczałem kolejne punkty które będą brane do elementów tego ciągu

	8π
I jak łatwo zauważyć ... od niebieskiego wszystko się powtarza ( bo		= 2π)
	4

więc mamy 8 różnych punktów na krzywej cos(nπ/4). Zauważ, że (−1)ⁿ przyjmuje tylko dwie wartości ... −1 lub 1 jako że mnożymy tę wartość przez 4 (a wartość cosinusa jest nie większa niż 1 i nie mniejsza niż −1) to wiemy, że 4*1 oraz 4*(−1) będzie miała GŁÓWNY wkład w wartość granicy górnej i dolnej tak więc ... granica górna będzie dla jakiegoś 'n' parzystego (więc wybieram taki dla którego cosinus przyjmuje największą wartość ... najlepiej = 1) natomiast dolna granica będzie dla jakiego 'n' nieparzystego (więc wybieram taki dla którego cosinusów przyjmuje najmniejszą wartość ... najlepiej = −1 ale to jest niemożliwe ... więc biorę taki n dla którego wartość cosinusa będzie równa −√2/2)

wredulus_pospolitus: mokła to dziewczyna stojąc na deszczu

Adelajda: Przepraszam ale jakoś mało co z tego zrozumiałam, mógłbyś to jeszcze raz napisać? Znaczy się rozumiem czemu zaznaczamy 8 pkt ale czemu w dolnej te "+3"?

wredulus_pospolitus: dlaczego bierzemy 8k rozumiesz (aby mieć wielokrotność 2kπ w cosinusie) no to jedziemy po kolei:

	8kπ + 0π
8k + 0 : a8k + 0 = 4*(−1)8k+0 + cos(		) = 4*1 + cos(2kπ + 0) =
	4

= 4 + 1

	8kπ + 1π
8k + 1 : a8k + 1 = 4*(−1)8k+1 + cos(		) = 4*(−1) + cos(2kπ + π/4) =
	4

= −4 + √2/2

	8kπ + 2π
8k + 2 : a8k + 2 = 4*(−1)8k+2 + cos(		) = 4*1 + cos(2kπ + 2π/4) =
	4

= 4 + 0

	8kπ + 3π
8k + 3 : a8k + 3 = 4*(−1)8k+3 + cos(		) = 4*(−1) + cos(2kπ + 3π/4) =
	4

= −4 −√2/2

	8kπ + 4π
8k + 4 : a8k + 4 = 4*(−1)8k+4 + cos(		) = 4*1 + cos(2kπ + 4π/4) =
	4

= 4 −1

	8kπ + 5π
8k + 5 : a8k + 5 = 4*(−1)8k+5 + cos(		) = 4*(−1) + cos(2kπ + 5π/4) =
	4

= −4 − √2/2

	8kπ + 6π
8k + 6 : a8k + 6 = 4*(−1)8k+6 + cos(		) = 4*1 + cos(2kπ + 6π/4) =
	4

= 4 + 0

	8kπ + 7π
8k + 7 : a8k + 7 = 4*(−1)8k+7 + cos(		) = 4*(−1) + cos(2kπ + 7π/4) =
	4

= −4 + √2/2 8k+8 już nie bierzemy bo to jest przecież inaczej 8(k+1) + 0. Więc wypisaliśmy wszystkie możliwe wartości jakie mogą przyjąć elementy tego ciągu. Jaka będzie granica dolna a jaka będzie granica górna

Marcel: Największa liczba jest dla "8k + 0" czyli to jest górna granica a dolna dla −4 − √2/2 bo to najmniejsza liczba, dziękuje ślicznie za pomoc!

Adelajda: Znaczy tak jak kolega u góry napisał?XD WTf

wredulus_pospolitus: to teraz rozumiemy dlaczego brałem 8k+3 ? I później napisałem że mogliśmy brać także 8k+5

Adelajda: Tak tak, już wiem o co chodzi, jak zawsze jesteś NIEZAWODNY!