sterometria abc: Podstawą graniastosłupa prostego jest romb o kącie ostrym 60. Krótsza przekątna graniastosłupa i przekątna ściany bocznej wychodzącej z jednego wierzchołka przecinają się pod kątem któego cosinus wynosi 2/3. Oblicz długość krawędzi tej bryły wiedząc że jej objętość wynosi 250√6 dm³. Ma ktoś pomysł, bo nie wiem jak się do tego zabrać

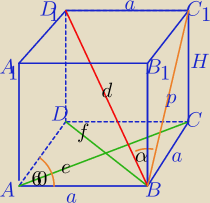
Mila: 1) f=a

	2
cosα=
	3

	a2√3
PABCD=a2*sin 60o=
	2

	a2√3
V=		*H
	2

a2√3
	*H=250√6⇒a2*H=500√2
2

2) Przekątne: d²=H²+f²⇔d²=H²+a² p²=a²+H² 3) W ΔDBC₁: a²=p²+d²−2*p*d cosα

	2
a2=H2+a2+H2+a2−2*√(H2+a2)*√(H2+a2)*
	3

	4
a2=2H2+2a2−		*(H2+a2)⇒
	3

a²=2H²

	a
H=
	√2

3) a²*H=500√2

	a
a2*		=500√2 /*√2
	√2

a³=500*2 a=10

	10
H=		=5√2
	√2

============== Sprawdź rachunki.

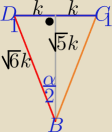Eta: Można też tak ( korzystam z rys, Mili ΔBDD₁≡ΔBCC₁ z cechy (bkb) to d=p ⇒ΔD₁C₁B −− równoramienny

	α		2		α		5
cosα=2/3 ⇒ 2cos2		−1=		⇒ cos2		=
	2		3		2		6

	α		√5k		a
cos		=		to		=1k ⇒ a=2k
	2		√6k		2

W ΔBCC₁ z tw, Pitagorasa H²= 6k²−4k² ⇒ H=√2k

	√3
V= 4k2*		*√2k =250√6 ⇒ k3=125 ⇒ k=5
	2

Odp: a=2k=10 , H=√2k=5√2 =========================

Mila: abc dalej płacze

Eta: Jak się wypłacze ,to wróci