liczby zespolone
zespolont: z−|z| = 1−2i
jak rozprawic sie z takim rownaniem?
2 lis 18:56
sushi:
z=x+iy
podstaw i potem porównaj odpowiednie liczby
2 lis 18:58
zespolont: własnie tak rozpisuje, ale wychodzi mi sprzecznosc...
2 lis 19:03
sushi:
zapisz swoje obliczenia
2 lis 19:06
zespolont: pisze z telefonu wiec ciezko moze byc no ale sproboje
x+iy − √x2+y2 = 1 − 2i
y = −2
x−√x2+4=1
i mam x= −1,5 ale jak podstawiam do wyjsciowego wychodzi mi −4=1
2 lis 19:11
sushi:
po przekształceniu
x−1= √x2+4
założenie jakie musi być x......, aby można było podnieść obustronnie do kwadratu
(x−1)2= x2+4
x2−2x+1=x2 +4
−2x=3
x=−1,5 + założenie i wychodzi sprzeczność
teraz pytanie czy przykład dobrze zapisany ?
2 lis 19:17
sushi:
a jakbyśmy nie podstawiali
założenie x≥1
(x−1)2= x2+y2
−2x+1= y2 i teraz to narysować
2 lis 19:20
sushi:
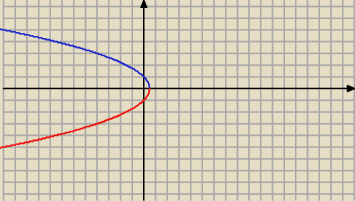
2 lis 19:24
zespolont: przykład przepisany dobrze, czyli co wychodzi ze brak rozwiazan?
2 lis 19:24
sushi:
już z tego x− √x2+y2 co daje liczbę niedodatnią, a po prawej stronie równania jest
1
2 lis 19:28
zespolont: racja, czyli mialem dobrze ale nie sadzilem ze to bedzie odpowiedz

2 lis 19:31
Mila:
z−|z| = 1−2i
z+2i=1+|z|
x+iy+2i−1=
√x2+y2, gdzie x,y∊R
(x−1)+i*(y+2)=
√x2+y2
y+2=0
y=−2
x−1=
√x2+4
x≥1
x
2−2x+1=x
2+4
−2x−3=0
brak rozwiązań
2 lis 19:34

