trójkąt PMP: Na przeciwprostokątnej AB trójkąta prostokątnego ABC obrano punkt M tak,że miara kąta BMC jest dwa razy większa od miary kąta BCM Wykaż,że zachodzi równość

1		1		2
	+		=
AM		BM		CM

jc: Jakiś mały błąd w treści.

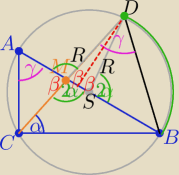
Eta: |AB|=2R , |DS|=|DM|=R ( bo ΔDMS jest równoramienny |∡BSD|=2α=|∡DMA| ΔACM ∼ ΔBMD z cechy (kkk) to

|CM|		|BM|		|CM|		|AM|
	=		i		=
|AM|		|MD|		|BM|		|DM|

dodając stronami otrzymujemy:

CM		CM		AM+BM		2R
	+		=		=		=2 / : CM
AM		BM		DM		R

mamy tezę

	1		1		2
		+		=
	AM		BM		CM

================

jc: To ja źle przeczytałem, ale za to mam takie zadanie: Pokazać, że jeśli miary kątów ACM i BCM są równe, to

1		1		2
	+		=
AM2		BM2		CM2