relacje salamandra: Wyznacz klasy abstrakcji relacji a) {(a,a), (b,b), (c,c), (a,b), (b,a)} ∊ {a,b,c} jak się za to zabrać? mam powyżej podany przykład do klasy abstrakcji, z którego nie potrafię nic wynieść do tego konkretnego zadania: https://ibb.co/J3KQ5QV

ABC: przyswoiłeś teorię ? wiesz że klasy abstrakcji są niepuste i rozłączne?

salamandra: To, co wysłałem, jest jedyną teorią, którą "dostaliśmy" od prowadzącego ćwiczenia.

jc: Tam powinno być ... ⊂ {a,b,c}² [a] = klasa abstrakcji elementu a. x ∊ [a] ⇔ x jest w relacji z a [a]=[b]={a,b}, [c]={c}

salamandra: Dlatego stąd Twoje stwierdzenie, że trzeba mieć do mnie końskie zdrowie, bo muszę się sam wszystkiego uczyć od zera i ten materiał, który aktualnie przyswajam, który będzie jutro dopiero wprowadzany na ćwiczeniach, wyprzedza wykład o dobre dwa tygodnie. Na wykładzie miałem dopiero ledwo zaczęte funkcje, gdzie zadania z funkcji musiałem już mieć zrobione na tamten poniedziałek.

salamandra: @jc, przepisałem, tak jak mam w poleceniu, w takim razie jest błąd.

jc: Ściągnij sobie znakomitą książeczkę: Gleichgewicht B. − Elementy algebry abstrakcyjnej

jc: Relacja to podzbiór iloczynu kartezjańskiego, czyli zbiór par.

salamandra: czyli tą klasą abstrakcji będzie w tym przypadku to wszystko, co łączy się z "a", czyli [a]={a,b}, z [b] tak samo i z c łączy się tylko c, tak?

jc: Tak.

salamandra: b) {(a,b) ∊ R²: ∃_n∊Zn ≤ a < n+1 ⋀ n ≤ b < n+1} Po pierwsze− czemu R²? a nie R? [a]=<n;n+1) [b]=<n;n+1)?

jc: Tu R nie oznacza relacji, tylko zbiór liczb rzeczywistych. a jest w relacji z b ⇔ część ułamkowa a = część ułamkowa b [a] = [ podłoga(a), podłoga(a)+1 ) np. [π] = [3,4) [5]=[5,6) itd.

salamandra: Przepraszam, ale jaka „podłoga”?

ABC: gościu chcesz być informatykiem i nie znasz funkcji " podłoga" i "sufit" ? doczytaj szybko

salamandra: nie rozumiem jakie zastosowanie ma tutaj "_"

salamandra: podłoga* (forum nie odczytuje, a chciałem zabłysnąć, że jednak wiem, co to podłoga )

jc: W poprzednich zadaniach pisałeś (a,b) ∊ R. R oznaczało relację. W tym zadaniu (a,b) ∊R², a R oznacza zbiór liczb rzeczywistych.

jc: Część całkowita, ale od pewnego czasu często mówi się podłoga. Zobacz do wiki, jak się oznacza, bo tu nie ma odpowiedniego oznaczenia.

jc: https://pl.wikipedia.org/wiki/Podłoga_i_sufit

salamandra: Po czym wnioskujesz, że trzeba tutaj patrzeć na jakieś części ułamkowe i czemu ta klasa abstrakcji to [podłoga(a), podłoga(a)+1)?

salamandra: Ok, już chyba wiem

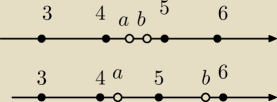
jc: Na pierwszym rysunku a i b należą do tej samej klasy, bo istnieje odpowiednie n, a mianowicie n=4. Na drugim rysunku a i b należą do różnych klas.