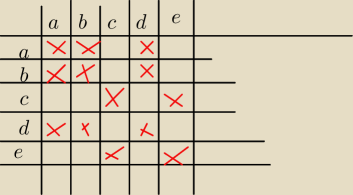
relacje salamandra: Które z własności spełnia relacja przedstawiona na grafach?: https://ibb.co/XtmJtVY a) symetryczna, zwrotna, przechodnia

wredulus_pospolitus: symetryczna −−− jasne zwrotna −−− także przechodnia −−− także

salamandra: b) symetryczna, przechodnia?

wredulus_pospolitus: Graf (2) symetrycznośc −−− jasne zwrotność −−− nie (chociazby dla 'b' nie ma) przechodność −−− nie (chociażby a −> d , d −> b ale już nie ma a −> b)

salamandra: @wredulus −−− nie mam do wyboru tylko spośród symetrycznej, zwrotnej i przechodniej, tylko to była odpowiedź do przykładu a)

wredulus_pospolitus: (c) nie jest zwrotna i symetryczna, ale jest przechodnia

salamandra: z tą przechodniością właśnie nie bardzo rozumiem, wczoraj ite próbowała mi to rozpisać i bazowaliśmy np. na relacji {(a,a), (b,b), (a,b)} i że tu istnieje przechodniość, ponieważ a−>b, b−>b i a−>b, jakoś zakładając, że x=a, y,z=b

salamandra: c) przechodnia, przeciwzwrotna, antysymetryczna albo nawet przeciwsymetryczna?

wredulus_pospolitus: (d) zwrotna − tak symetryczna − nie przechodnia − nie

salamandra: wytłumaczyłbyś w tym b) dlaczego nie jest przechodnia? Niby relacja {(a,a)} też jest przechodnia, więc czy nie mógłbym w b) założyć, że np. rozpatruję a−>d, d−>a, a−>a?

wredulus_pospolitus: co do przechodności R₁ −−− relacja wzrostu .... x R₁ y gdy piłkarz x jest niższy od piłkarza y no i oczywiście jest że x R₁ y oraz y R₁ z no to x R₁ z R₂ −−− relacja 'zwycięskiego klubu' ... x R₂ y gdy klub x wygrał mecz z klubem y x R₂ y oraz y R₂ z nie oznacza, że x R₂ z, nieprawdaż ?!

wredulus_pospolitus: @Salamandra ... realacja jest przechodnia jeżeli DLA DOWOLNEJ trójki zachodzi przechodność. bo w przeciwnym razie to równie dobrze każda relacja zwrotna byłaby przechodnia: a −> a ; a −> a ; no to a − > a

salamandra: aha, no i tego słowa zabrakło, "DLA DOWOLNEJ" Czyli w b) po samym tym, że a,b,c i się w jakikolwiek sposób nie łączą już można przechodniość odrzucić?

ABC: tak skutkuje wyrzucenie elementów logiki matematycznej z programu szkoły średniej

wredulus_pospolitus: tak jak napisałem ... w grafie (b) znalazłem taką 'ścieżkę' gdzie mogę przejść z a do d, później z d do b ... ale nie ma bezpośredniej drogi z a do b z tego powodu ... relacja ta nie jest przechodnia.

salamandra: ok, dzięki

wredulus_pospolitus: (c) przecież jest przechodnia to jest skierowany graf pełny K₅. Trzeba chwilkę popatrzeć czy aby na pewno jest dobrze, ale jest dobrze

salamandra: miałem na myśli, że w przykładzie b) biorąc literki a,b,c sam przecież napisałem, że c) jest przechodnia