zadanie z treścią ano: Marcin zbierał podpisy na poparcie petycji, chodząc po kolei do stojących przy ulicy Miodowej 50 domów. Petycję w każdym domu podpisała co najmniej jedna osoba. Marcin łącznie zdobył 90 podpisów. Wykaż, że przy ulicy Miodowej możemy znaleźć kilka sąsiednich domów, w których Marcin zdobył dokładnie 7 podpisów. [zasada szufladkowa]

kerajs: A ile to jest kilka? Jeśli kilka=3 to teza nie jest prawdziwa, ale dla kilka>3 już jest.

wredulus_pospolitus: k=4 także nie jest wystarczającą ilością: 2,2,1,1,2,2,1,1,... ale podejrzewam, że 'kilka' to bliżej nieokreślona liczba (od 1 do 7 włącznie)

wredulus_pospolitus: inny podział: 4,8,8,8,8,8,1,...., 1,1,1,1

Umanus: Obstawiam, że kilka znaczy >2. Tylko co dalej?

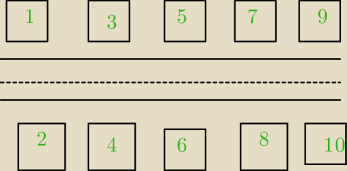
getin: czy domy 1 i 3 są sąsiednie ? czy 5 i 6 też są sąsiednie ? Nieprecyzyjne polecenie "sąsiednie domy", więc biorą się wątpliwości

a7: moim zdaniem chodzi o kilka kolejnych domów

a7: raczej chodził najpierw po jednej stronie ulicy potem po drugiej

wredulus_pospolitus: @a7 i @getin ... najprawdopodobniej autorowi zadania chodziło o ciąg domów po jednej stronie ulicy. W momencie gdy bierzemy pod uwagę domy po obu stronach ulicy, ale 'sąsiednie' nie oznacza przejście przez ulicę to można 'dopiąć swego' z kontrprzykładem (poniżej pokazane ustawienie przy założeniu że mamy 2x 25 domów) 1,1,1,1,1,1,7,1,1,1,1,1,1,7,1,1,1,1,1,1,7, 1,1,1,3 1,1,1,1,1,1,7,1,1,1,1,1,1,7,1,1,1,1,1,1,7, 1,1,1,3

wredulus_pospolitus: Nie sądzę, aby to zadanie mówiło o domach po obu stronach ulicy. Nawet jako zadanie dodatkowe (a zapewne takie to właśnie jest) raczej samo ustawienie domów 'gęsiego' jest wystarczająco problematyczne dla większości uczniów.

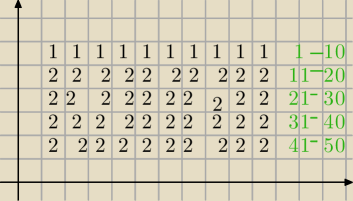
a7: chyba nie rozumiem treści pytania/zadania, bo w takim układzie (jak na rysunku) to ja nie widzę, gdzie by zdobył dokładnie 7 głosów w kilku sąsiednich domach a gdyby w domach 1−49 zdobył po 1 głosie a w 50−tym 41 głosów to co? to przecież te jedynki też się zsumują do siódemki, czy ktoś mógłby rozjaśnić treść zadania?

a7: czyli 11111171111117111111711111171111117111111711111171 i jest kontrprzykład tak?

a7: no prawie

wredulus_pospolitus: gdyby sumą nie było 92

a7: ale czy w treści zadania chodzi o toże ma być kilka domów z 7−mioma głosami koło siebie? czyże w kilku domach kolejnych kolo siebie głosy sumują się do siedmiu?

a7: jeśli chodzi o ulicę Miodową (w wawie) to nie wiem czy ona w ogóle ma tyle numerów, żeby szedł po jednej stronie ulicy....

a7: w dawnej stolicy Polski ulica Miodowa ma więcej numerów, więc wychodzi na to, że jeśli Marcin zbierał podpisy w Wawie to da się przedstawić kontrprzykład (godz. 11:05 ?) a jeśli w Krakowie to rzeczywiście w kilku domach ilość głosów będzie się w paru domach sumowała do 7 (?) (?)/ będzie wynosiła 7 (?) /ja mam wątpliwości co do treści zadania, więc być może ten post jest trochę nieścisły/

a7: PS.np we Wrocławiu Miodowa tez ma więcej numerów po jednej stronie

ano: Jeśli dobrze rozumiem, mamy założyć, że domu są ustawione jeden po drugim, wzdłuż prostej, bez przechodzenia na drugą stronę.

a7: @ano, ale czy chodzi o to że w kilku domach było dokładnie siedem podpisów, czyże suma podpisów w kolejnych domach była 7?

wredulus_pospolitus: @a7 −−− by suma w iluś kolejnych domach dała dokładnie 7

ano: Nie mieliśmy powiedziane tego na zajęciach, ale z treści zadania wnioskuję, że ma być dokładnie 7 w kilku kolejnych. Tylko według mnie to nie ma prawa działać.

a7: no to wykazane przecież, że nie da się wymyślić kontrprzykładu w najbardziej "sprzyjających" warunkach może być w sześciu domach pod rząd 1 głos za potem aby się nie sumowało do 7 musi być 7 i tak ileś razy i widzimy, że w 50−ciu domach suma przekroczy 90 głosów, bo będzie ich 92, jak napisał wredulus czyli już wcześniej któreś dwie siódemki lub inna ilość głosów w którymś domu musi być mniejsza niż 7 a wtedy sąsiadując z jedynkami będzie suma 7 jeśli weźmiemy inne liczby przykładowo dwójki, trójki, czwórki czy piątki to choćby nie wiem jak się natęzał nie znajdziemy takiego układu w szufladkach (domach) by co najmniej trzy sumy nie były 7 (dwie sąsiednie) 11111171111117111111711111171111117111111711111171 =92 11111161111117111111711111171111117111111711111161 =90

ano: Okej, a gdyby jednak założyć, że to suma ma nam dać 7?

a7: to będzie tak, jak pisałam 16:09, jeśli w kilku kolejnych miałoby być 7 to kontrprzykład jest 11:10

ano: Da się jakoś formalniej udowodnić, że w przypadku doboru np. 2 3 itd ta suma zawsze dojdzie do 7?