relacje
salamandra: 3.Które z własności spełnia relacja:
c) {(a,b) ∊ R: a=2b v b=2a}
np. (0,0), (1,2), (2,1), (2,4), (4,2)
więc: symetryczna
d) {(m,n) ∊ N: m=n+1 mod 4}
np. (0,3), (1,4), (2,1), (3,2), (2,5)
więc: przeciwzwrotna
e) {(m,n) ∊ Z: m+n=3}
np, (1,2), (2,1), (0,3), (3,0), (−1,4), (4−1)
więc: przeciwzwrotna, symetryczna
4. Które z własności spełnia relacja przedstawiona na grafie?
https://ibb.co/XtmJtVY
a) symetryczna, zwrotna, przechodnia
b) symetryczna
c) przechodnia, przeciwzwrotna, antysymetryczna
d) zwrotna, przechodnia, antysymetryczna
dobrze?
1 lis 10:30
sushi:
zrobiłaś może tabelkę, aby sprawdzić czy może robiłaś na podstawie wzorów ?
1 lis 10:35
salamandra: nie robiłem na podstawie żadnych wzorów, ani tabelek
1 lis 10:36
sushi:
to tak ma "pałę" podałaś odpowiedzi do zadania 3?
1 lis 10:38
salamandra: no nie na pałę, jak widzisz, napisałem poniżej kilka przykładów takich par i na podstawie tego
wyciągałem wnioski.
1 lis 10:41
sushi:
ja tam wolę np tabelkę i w środku zaznaczam krzyżykiem, te pary liczb, które pasuję
wtedy widać od razu symetryczność i zwrotność, dorzucając "znajomość wzorów" też widać
pozostałe własności
nie wypisałaś dlaczego nie mogą być inne własności
1 lis 10:48
salamandra: A ja mam za zadanie sam to ogarnąć, bez pomocy prowadzącego ćwiczenia, nie mam podanych żadnych
wzorów do materiałów, żadnych tabelek i muszę sobie radzić za pomocą samych definicji, nie
wiem o żadnych tabelkach i wzorów, byłbym wdzięczny, gdybyś mi podała/podał chociaż przykład,
jak za pomocą tych tabelek/wzorów to rozwiązać.
1 lis 10:51
sushi:
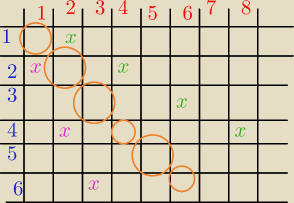
na kółkach muszą być "x" aby była zwrotna
aby podać, że nie zachodzi jakaś własność trzeba podać pary liczb, inaczej na uczelni nie
zaliczą zadania
1 lis 10:55
salamandra: Jeszcze dopytam− któryś konkretnie podpunkt tutaj został rozwiązany?
1 lis 10:58
1 lis 10:59
sushi:
to był "a=2b lub b=2a" dlatego dałem różne kolory
1 lis 10:59
salamandra: Ok, tak myślałem, ale nie widziałem, aby "0" zostało uwzględnione, więc wolałem dopytać. Jesteś
w stanie mi odpowiedzieć, czy dobrze rozwiązałem pozostałe?
1 lis 11:00
sushi:
xgy (x w relacji z y) −> czyli relacja g
ygx (y w relacji z x) −> czyli relacja g−1
− zwrotna
xgx czyli z tabelki musi być zakreślona cała przekątna (zwana Δ)
− symetria
g o g−1 ⊂ g czyli krzyzyki pod przekątną muszą być symetrycznie też nad przekątna
− przeciwsymetryczna (asymetryczna)
g ∩ g−1 = ∅
− przeciwzwrotna
Δ ∩ g = ∅
− spójna
g ∪ g−1= X cała tabelka
− antysymetryczna
g ∩ g−1 ⊂ Δ
1 lis 11:07
sushi:
do 3 c) pokaż po kolei że dana własność zachodzi/niezachodzi
1 lis 11:09
salamandra: c) zwrotna zachodzi tylko dla (0,0), więc odpada, bo musiałaby zachodzić dla każdej pary
przeciwzwrotna zachodzi dla wszystkich oprócz (0,0), więc również odpada
symetryczna zachodzi dla każdej pary, tj. (0,0), (1,2), (2,1), (2,4), (4,2) itd
antysymetryczna nie zachodzi, wystarczy podać parę (1,2), (2,1).
przechodnia nie zachodzi, bo nie ma takiej pary, dla której xRy, yRz i xRz.
1 lis 11:12
sushi:
c)
−zwrotna nie ( bo nie jest cała przekątna "zaiksowana")
−przeciwzwrotna nie ( bo jest (0,0)∊g, a nic nie może być na przekątnej) patrz−> Δ ∩ g = ∅
−symetryczna tak g= g−1
− przeciwsymetryczna − nie bo g−1=g patrz −> g ∩ g−1 = ∅ oraz jak jest symetryczna, to
nie moze być przeciwsymetryczna ani antysymetryczna
− antysymetryczna − nie −−> g ∩ g−1 ⊂ Δ "cześć wspolna nie siedzi na przekatnej) +
komentarz powyżej
−przechodnia g o g−1 ⊂ g u góry zgubiłem − nie bo (1,2) o (2,1)= (1,1) ∉ g
−spójna − nie
1 lis 11:21
sushi:
d) m≡ n+1 (mod 4) ?
1 lis 11:23
salamandra: właśnie nie wiem czy ja to dobrze czytam, bo to n+1 ma być tą resztą z dzielenia, czy liczbą,
którą dopiero przez 4 będę dzielił? według mnie n+1 jest liczbą, którą będę dzielił, a "m"
jest tą resztą, przynajmniej tak jest w informatyce, ale w dalszych zadaniach mam jakieś klasy
abstrakcji i tam dziwnie jest ten mod przedstawiony, później podeślę.
1 lis 11:25
sushi:
raczej to co ja zapisałem
a≡b (mod n) <=> n| (a−b)
dlatego tutaj polecam zrobić tabelkę od 0 do 10 po "m" i "n" i na rysunku wyjdzie ładne
położenie "x"
to potem moze się przydać do klas abstrakcji
1 lis 11:31
salamandra: może zanim zrobię tę tabelkę, to spytam: pary np. (0,3), (1,4) są dobrze?
1 lis 11:32
sushi:
tak, dla modułów trzeba brać (0,3), (0,7), (0,11)......
(1,4) nie jest pierwszą parą dla (1,....)
1 lis 11:37
salamandra:
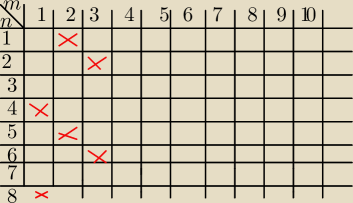
1 lis 11:40
sushi:
za mało krzyzyków
jeżeli 0 ∊N, to tabelka powinna być od "0"
(m\n) u Ciebie jest (n\m) zamienić kolejność "m" z "n" w tabelce
(0,3), (0,7), (0,11)......
(1,0), (1,4), (1,8) (1,12)....
(2,1), (2,5), (2,9),....
(3,2), (3,6), (3,10),...
(4,3), (4,7), (4,11),...
1 lis 11:48
salamandra: tak, wiem, że za mało, ale nie mogłem zmieścić tylu kolumn i wierszy, ale wiem o co chodzi
1 lis 11:52
salamandra: i u mnie poziomo są "m", a pionowo "n", czyli dobrze
1 lis 11:53
sushi:
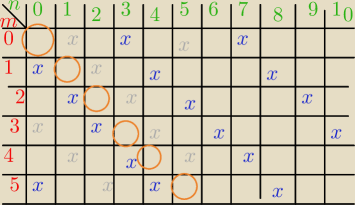
1 lis 11:54
sushi:
x −> relacja g
x −−> relacja g−1
1 lis 11:55
sushi:
lepiej tak robić bo od razu widać klasy abstracji, jak relacja będzie: "zwrotna, symetryczna,
przechodnia"
1 lis 11:56
salamandra: czyli ta będzie tylko przeciwzwrotna, tak jak napisałem?
1 lis 12:01
sushi:
a przeciwsymetryczna ?
1 lis 12:02
salamandra: no tak, racja
1 lis 12:04
sushi:
a antysymetryczna ? g ∩ g−1 ⊂ Δ
1 lis 12:06
salamandra: a czym się różni antysymetryczna od przeciwsymetrycznej? nie zauważyłem, że pytałeś o
przeciwsymetryczną, a ja miałem na myśli, że ona jest antysymetrcyzna
1 lis 12:07
sushi:
− przeciwsymetryczna (asymetryczna)
g ∩ g−1 = ∅
− antysymetryczna
g ∩ g−1 ⊂ Δ
1 lis 12:09
sushi:
z linku
antysymetryczność (słaba antysymetryczność),
(x ϱ y) ∧ (y ϱ x) ⇒ x = y ,
przeciwsymetryczność lub asymetryczność (ścisła antysymetryczność),
(x ϱ y )⇒ ¬ ( y ϱ x ) ,
1 lis 12:12
salamandra: aaa, czyli antysymetryczna jest wtedy, gdy symetryczność istnieje tylko pomiędzy identycznymi
elementami, a przeciwsymetryczność, jak nawet dla równych nie występuje, a ściślej− nie
posiada równych?
1 lis 12:18
sushi:
antysymetria == jak weźmiesz (1,4) i (4,1) −−> (1,1) , gdzie (1,4) ∊ g, (4,1) ∊ g−1
przeciwsymetryczność === (1,4) ∊ g, a (4,1) ∉ g−1
lub z tego co napisalem o 12.09
1 lis 12:22
sushi:
antysymetria == jak weźmiesz (1,4) i (4,1) −−> (1,1) , gdzie (1,4) ∊ g, (4,1) ∊ g−1
przeciwsymetryczność === (1,4) ∊ g, a (4,1) ∉ g−1
lub z tego co napisalem o 12.09
1 lis 12:22
salamandra: nie rozumiem na podstawie takich definicji − czy to co powiedziałem o 12:18 jest poprawne?
Jak mam jakieś pary: (1,2), (2,1), (2,4), (4,2)− to mamy symetrie, a jak mamy (1,3), (2,4),
(3,3), (4,4) to mamy antysymetrię.
Jak mamy (1,3), (2,4), (5,6) to mamy przeciwsymetrię tak?
1 lis 12:25
sushi:
przeciwsymetryczność === (1,4) ∊ g i (4,1) ∉ g ==> (1,4) ∊ g−1
1 lis 12:25
salamandra: to w końcu w tym przykładzie d) będzie przeciwsymetryczna tak?
1 lis 12:30
sushi:
patrz na teorię
antysymetryczność (słaba antysymetryczność),
(x ϱ y) ∧ (y ϱ x) ⇒ x = y ,
+ pomocnicze (z tabelki)
g ∩ g−1 ⊂ Δ
poza tym trzeba sprawdzić każdą parę, a nie rzucasz parami i zrozumieć te dwa wzory powyżej
1 lis 12:30
salamandra: czyli dla każdej tabelki muszę/powinienem sobie pomocniczo dopisać krzyżyki z g−1?
1 lis 12:32
sushi:
− przeciwsymetryczna (asymetryczna)
g ∩ g{−1} = ∅
Czy "x" niebieskie i szare się pokrywają ?
aby była przeciwsymetryczna "część wspólna" musi dać zbiór pusty ?
Czyli prośćiej mówiąc, aby była to relacja przeciwsymetryczna "x" nie mogą się pokrywać
1 lis 12:33
sushi:
tabelka jest dla ułatwienia oraz moje wzory;
zrobisz sobie innym kolorem "g−1" i bedzie widać wszsytkie własności jak na tacy
normalnie jedziesz z "linka" gdzie nie zawsze widać i strzelasz przy tych trudnych.
1 lis 12:35
salamandra: już chyba zrozumiałem, czyli Δ to ta cała przekątna, ale żeby była antysymetryczna to musi się
ZAWIERAĆ w tej delcie, ale niekoniecznie całej tak?
1 lis 12:36
sushi:
Δ− pisałem o tym na samym początku
częśc wspólna "x" szarych i niebieskich musi się zawierać w Δ

nigdzie nie jest napisane g ∩ g
−1= Δ
1 lis 12:42
salamandra:
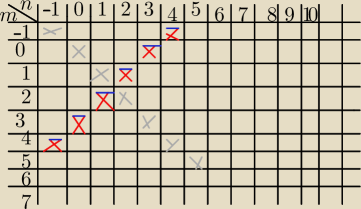
e) przeciwzwrotna, symetryczna
niebieska kreska= g
−1
1 lis 12:43
sushi:
tutaj można wyjść od działania
x+y= 3 (dodawanie jest przemienne) więc y+x= 3 −−> symetryczna , więc już odpada
antysymetryczna i przeciwsymetryczna
zwrotna nie jest
spojna nie jest
przechodnia nie jest
zostaje do sprawdzenia "przeciwzwrotność" (teoria lub tabelka i moje wzory)− tak
1 lis 12:49
sushi:
zadanie "4" załóż nowy post, dodatkowo wypisz jakie pasują pary oraz mozna zrobić tabelkę

1 lis 12:49
salamandra: 
dzięki za pokazanie tego sposobu z tabelką, faktycznie ułatwia sprawę.
A jak z tymi grafami, co podesłałem link do zdjęcia?
1 lis 12:50
salamandra: sory, pisałem, zanim zobaczyłem 12:49.
1 lis 12:51
sushi:
na zdrowie

1 lis 13:04
 na kółkach muszą być "x" aby była zwrotna
aby podać, że nie zachodzi jakaś własność trzeba podać pary liczb, inaczej na uczelni nie
zaliczą zadania
na kółkach muszą być "x" aby była zwrotna
aby podać, że nie zachodzi jakaś własność trzeba podać pary liczb, inaczej na uczelni nie
zaliczą zadania


 nigdzie nie jest napisane g ∩ g−1= Δ
nigdzie nie jest napisane g ∩ g−1= Δ
 e) przeciwzwrotna, symetryczna
niebieska kreska= g−1
e) przeciwzwrotna, symetryczna
niebieska kreska= g−1

 dzięki za pokazanie tego sposobu z tabelką, faktycznie ułatwia sprawę.
A jak z tymi grafami, co podesłałem link do zdjęcia?
dzięki za pokazanie tego sposobu z tabelką, faktycznie ułatwia sprawę.
A jak z tymi grafami, co podesłałem link do zdjęcia?
