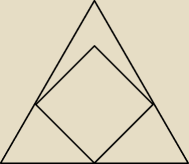
Wyznacz stosunek pola kwadratu do pola trójkąta równobocznego
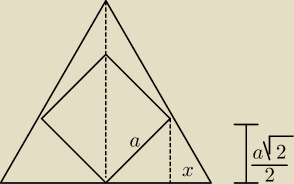
| x | √3 | √6 | |||||||||
= ctg60o = | −−−> x = a | ||||||||||
| 3 | 6 |
| √6 + 3√2 | ||
bok trójkąta = 2x + a√2 = a | −−−> Ptrojkata = .... | |
| 3 |
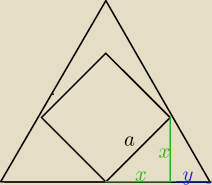Pole kwadratu =a2
| a√2 | ||
x√2=a czyli x= | (gdyż jest tam trójkąt równoramienny o bokach, x,x,a) | |
| 2 |
| y√3 | a√2 | |||
x= | czyli y√3/2= | czyli y=a√6/3 | ||
| 2 | 2 |
| 7 | ||
P trójkąta=b2√3/4= | a2√3 | |
| 6 |
| PKWADRATU | a2 | 2√3 | |||
= | =6/(√3*7)= | ||||
| PTRÓJKĄTA | 7/6a2√3 | 7 |
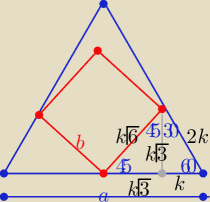a= 2k(√3+1) PΔ= k2√3(√3+1)2
b= k√6 P⬠= 6k2
| P⬠ | |
= ........... | |
| PΔ |
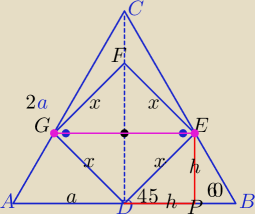1) |CD|=a√3
PΔABC=a2√3
2) |GE|=|DF|=2h
w ΔDPE:
x2=2h2
| |PB| | √3 | |PB| | ||||
W ΔPBE: ctg60o= | ⇔ | = | ||||
| |h | 3 | h |
| √3 | ||
|PB|= | *h | |
| 3 |
| √3 | √3 | |||
a=h+|PB|=h+ | *h=h*(1+ | ) | ||
| 3 | 3 |
| 3+√3 | ||
a=h* | ||
| 3 |
| 3+√3 | 12+6√3 | |||
PΔABC=a2√3=(h* | )2*√3=h2* | *√3 | ||
| 3 | 9 |
| 6*(2+√3)*√3 | 2h2*(2√3+3) | |||
PΔABC=h2* | = | |||
| 9 | 3 |
| P□ | 2h2 | 3 | |||||||||
= | = | ||||||||||
| PΔABC |
| 3+2√3 |
