Funkcja liniowa w trzech płaszczyznach bartek2213: Witam, mam problem z podanym zadaniem. Dana jest prosta l : x = 1 + t y = −t z = 3 + t Oraz punkt A(1, −1, −2). Wyznaczyć punkt B symetryczny do punktu A względem prostej l, oraz równanie płaszczyzny π zawierającej prostą l i punkty A i B. Czy ktoś mógłby dać mi wskazówkę w jaki sposób rozwiązać podane zadanie − nigdy nie wykonywałem zadań gdzie użyte są trzy płaszczyzny zamiast dwóch. Czy jest jakieś źródło gdzie mógłbym zobaczyć przykłady zadań w trzech płaszczyznach i ich rozwiązania?

ABC: gdzie ty tu widzisz trzy płaszczyzny? wymień je od 1 do 3

Jerzy: Piszesz równanie płaszczyzny prostopadłej do danej prostej przechodzącej przez punkt A.Szukasz punktu przebicia,który jest środkiem odcinka AB.Wyznaczasz współrzędne punktu B ze wzorów na środek odcinka.

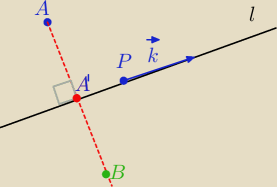
Mila: 1) Dana jest prosta l : x = 1 + t y = −t z = 3 + t P=(1,0,3)∊l, k^→=[1,−1,1] wektor kierunkowy prostej l 2) A' −Rzut prostopadły punktu A=(1, −1, −2) na prostą l A'=(1+t,−t, 3+t)∊l A=(1, −1, −2) AA'^→⊥k^→⇔ AA'^→ o k^→=0⇔ AA'^→=[t,−t+1, 3+t+2]=[t,−t+1,t+5] 1*t+(−1)*(−t+1)+1*(t+5)=0⇔

	4
t=−
	3

	1		4		5
A'=(−		,		,		)
	3		3		3

3) Współrzędne punktu B: A' jest środkiem AB

	1		1+xb
−		=
	3		2

4		−1+yb
	=
3		2

5		−2+zb
	=
3		2

oblicz wsp. punktu B 4) Napisz równanie szukanej płaszczyzny . Dasz radę sam?