Rozwiąż nierówność Gwar: Cześć. Mam problem z rozwiązaniem nierówności:

1		1
	<=
x3−x		|x|

Dla x<=0 wychodzą mi pierwiastki: −1 (nieparzystokrotne), 0 (parzystokrotne), 1 (nieparzystokrotne) Dla x>0 wychodzą mi pierwiastki: − √2, −1, 0, 1, √2 (tylko zero jest parzystokrotne) Oczywiście założenia są takie, że x nie równa się ani 0, ani −1, ani 1. Dla x<=0 wychodzi mi przedział x∊(−∞, −1>∪(1,+∞), ale tutaj nie uwzględniam tego, że moim wyjściowym założeniem na ten moment było x<=0. Bo gdybym to uwzględnił to chyba powinienem napisać x∊(−∞, −1>? Powinienem tak zrobić? Dla x>0, x∊(−∞,−√2>∪(−1,0)∪(0,1)∪<√2,+∞) albo x∊(0,1)∪<√2,+∞) jeżeli powinienem podawać wynik tylko dla x>0. Ostatecznie powinno mi wyjść: x∊(−∞, −1)∪(0,1)∪<√2,+∞), ale ja nie umiem tego zobaczyć w tych moich wyżej podanych przedziałach. Albo się pomyliłem gdzieś w liczeniu albo po prostu nie umiem połączyć tych przedziałów w jeden. Pomocy :C

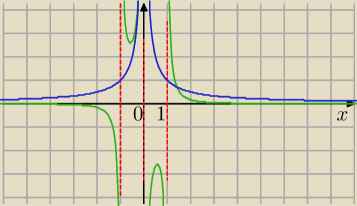
a7: I−wszy rysunek pomocniczy niebieska funckja 1/|x| zielona finkcja 1/(x³+x) (czerwone asymptoty pionowe)

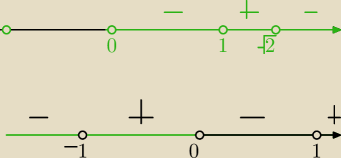
a7: dla x≥0 mamy

1		1
	≤
x(x2−1)		x

1		1
	−		≤0
x(x2−1)		x

	x2+2
		≤0 ||*[x*(x2−1)]2
	x(x2−1)

(x²+2)*x*(x²−1)≤0 x=0 lub x=1 lub x=−1 lub x=√2 lub x=−√2 (oś) x∊(0,1)∪(√2,∞) dla x<0 mamy

1		1
	≤−
x(x+1)		x

1		1
	+		≤0
x(x+1)		x

x2
	≤0 ||*[x(x2−1)]2
x(x2−1)

x³(x²−1)≤0 x=0 x=1 x=−1 x∊(−∞, −1) odp. x∊(−∞, −1)∪(0,1)∪(√2,∞) =====================

a7: tutaj link do innej nierówności wymiernej może to będzie pomocny przykład https://matematykaszkolna.pl/strona/2541.html

a7: albo może taki przykład będzie trafniejszy https://matematykaszkolna.pl/strona/3987.html

a7: a odpowiadają stricte na Twoje pytanie to tak powinieneś tak robić, że uwzględniasz tylko ten przedział który w danym "podpunkcie" rozwiązania bierzesz pod uwagę na koniec suma

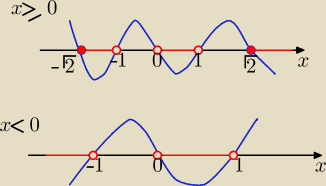
Eta: x∊R/{0,1,−1} dla x≥0

1		1
	−		≤0
x(x2−1)		x

	2−x2
		≤0
	x(x−1)(x+1)

x(x−1)(x+1)(√2−x)(√2+x)≤0 x∊<−√2, −1)U(0,1)U<√2,∞) dla x <0

1		1
	+		≤0
x(x2−1)		x

x2
	≤0
x(x−1)(x+1)

x³(x−1)(x+1)≤0 x∊(−∞,−1)U(0,1) suma przedziałów daje odpowiedź Odp: x∊(−∞, −1)U(0,1)U<√2, ∞) ===========================

Eta:

Gwar: Bardzo dziękuję za odpowiedzi. Przepraszam, że z takim poślizgiem, ale miałem problemy z internetem. Mimo to jestem bardzo, bardzo wdzięczny za pomoc.