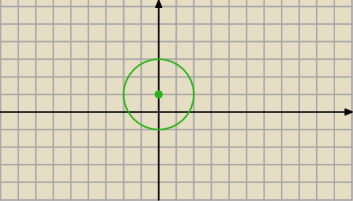
Liczby zespolone płaszczyzna gaussa Rafał: Witam mam naszkicować na pł. gaussa taką nierówność |z − i| ≤ 2 Jak zabrać się za ten moduł?

Jerzy: To jest koło o promieniu 2 i środku z = i

Jerzy:

Jerzy: Oczywiście trzeba zakreskować to koło.

Rafał: Skąd wiem że środek to z = i ?

Jerzy: |z − z₀| to odległość punktu z od punktu z₀ i tutaj masz: z_o = i Szukamy punktów z , których odległość od punktu z₀ = 1 jest nie wieksza niż 2 , czyli koło o takim promieniu i środku w punkcie z₀ = i

Rafał: Dziękuje, zrozumiałem

Rafał: A jak z takim przykładem? |z−i| / |z²+1| < 1

Jerzy:

	z − i
Zauważ,że: z2 + 1 = (z − i)*(z + i) , czyli:		< 1
	(z − i)(z + i)

Teraz dasz radę ?

Rafał: Czyli |z−i| / |z−1|*|z+1| < 1, |z−1| się skraca, mamy 1 / |z+1| < 1 ale co teraz?

Jerzy: Z założenia: x ≠ i i x ≠ −i , czyli: |z + i| > 0 Pomnóż obustronnie przez: |z + i|

Rafał: Czyli mam 1 < z+1, z > 0, więc zaznaczam wszystko powyżej osi X?

ABC: nie może być z>0 bo w liczbach zespolonych nie wprowadzisz relacji mniejsze/większe w rozsądny sposób gdzieś masz błąd w rachunkach

Jerzy: Coś ty się uparł z tą jedynką pod modułem ? Masz narysować : |z + i| < 1 , czyli: |z − (−i)| < 1

Rafał: Miałem 1 / |z+1| < 1 przemnożyłem i dostałem 1 < z+1 −> z > 0. Ja to tak rozumiem. Nie wiem dlaczego mam narysować |z+i| < 1 Uprałem się na tą jedynkę bo w mianowniku mam 1 a nie i

Jerzy: Upss .... ma być: |z + 1| > 1 , czyli rysujesz: |z − (−i)| > 1 . Potrafisz ?

Rafał: Czyli na układzie mam punkt (0, −1) i od tego punktu kółko o r = 1 i odpowiedzią jest wszystko oprócz tego koła?

Jerzy: Tak,to zewnętrze koła o środku z₀ = −i oraz promieniu 1

Rafał: Dzięki wielkie, zrozumiałem to.

ICSP: zewnętrze koła z wyłączeniem jednego punktu.