Jeszcze jedno z geometrii
DAniel: Wykaż, że jeśli punkt O jest punktem przecięcia się wysokości trójkąta ostrokątnego ABC, to
okręgi opisane na trójkątach ABC, AOC,AOB,BOC mają promienie równej długości
27 paź 20:22
Eta:
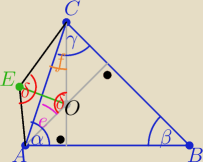
δ=180
o−f−e=180
o−(90
o−α)−(90
o−γ)= α+γ
β+δ= α+β+γ=180
o
to punkt E leży na okręgu opisanym na trójkącie ABC
i jednocześnie opisanym na trójkącie AEC
zaś ΔAEC≡ΔAOC
zatem R
ABC=R
AOC
analogicznie dla pozostałych trójkątów
i mamy tezę ...
27 paź 20:36
DAniel: Dzięki
27 paź 20:39
Eta:

27 paź 20:46
 δ=180o−f−e=180o−(90o−α)−(90o−γ)= α+γ
β+δ= α+β+γ=180o
to punkt E leży na okręgu opisanym na trójkącie ABC
i jednocześnie opisanym na trójkącie AEC
zaś ΔAEC≡ΔAOC
zatem RABC=RAOC
analogicznie dla pozostałych trójkątów
i mamy tezę ...
δ=180o−f−e=180o−(90o−α)−(90o−γ)= α+γ
β+δ= α+β+γ=180o
to punkt E leży na okręgu opisanym na trójkącie ABC
i jednocześnie opisanym na trójkącie AEC
zaś ΔAEC≡ΔAOC
zatem RABC=RAOC
analogicznie dla pozostałych trójkątów
i mamy tezę ...
