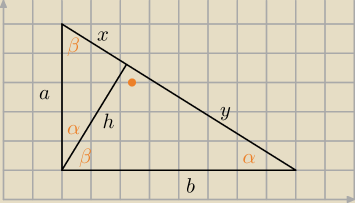
geometria DAniel: Oblicz długości odcinków przeciwprostokątnej na jakie dzieli ją wysokość poprowadzona w trójkącie prostokątnym jeśli wiadomo że suma długości przyprostokątnych wynosi m zaś stosunek długości szukanych odcinków wynosi k . Wynik przedstaw w najprostszej postaci.

Saizou : a+b = m →a²+b² = m²−2ab

y
	= k
x

Z podobieństwa trójkątów

x		a
	=
a		x+y

mx = a²

y		b
	=
b		x+y

my = b² Z tw. Pitagorasa a² + b² = (x+y)² mx+my = (x+y)² m = x+y I mamy układ

y
	= k → y = kx
x

m = x+y m = x+kx

	m
x =
	1+k

	km
y =
	1+k

DAniel: Ale m to jest a+b

a7: z podobieństwa trójkątów

x		a
	=		czyli a2=x(x+y) a2=x(x+kx) ⇒ a2=x2(k+1)
a		x+y

z tw. Pitagorasa a²=x²+h² h²=x²*k²x² czyli a²=x²+k²x⁴ ⇒a²=x²(x²k+1) przyrównujemy a² i mamy x²(k+1)=x²(x²k+1) czyli k+1=x²k+1 x²=1 x=1 y=k (?)

a7: u mnie źle

DAniel: no chyba nie

a7: źle bo h²=x*kx=kx² i masło maślane

DAniel: z tego co wiem to wyniki z pierwiastkami mają być

a7: po nowych wyliczeniach wyszło mi

	m(√k+1−√k2−k+2)		m(√k+1+√k2−k+2)
x1=		lub x2=
	k2−1		k2−1

a7: chyba to zadanko dla Mili lub Ety

a7: a znasz wyniki @DAniel?

jc:

	√1+k2
x=m		, y=kx?
	(1+√k)(1+k)

Eta: a+b=m a² +b²=x²(k+1)² z podobieństwa

x		b
	=		⇒ b=x√k+1
b		x(k+1)

kx		a
	=		⇒ a=x√k√k+1
a		x(k+1)

a²+b²=(a+b)²−2ab = m²−2x²√k(k+1)= x²(k+1)² zatem x²(k+1)(k+1−2√k)=m² x²(k+1)(√k+1)²=m²

	m		km
|AD| =x=		i |DB|=kx=
	√k+1*(√k+1)		√k+1*(√k+1)

=========================================

Eta: Poprawiam zapis : zatem ..... +2√k

DAniel: Dziękuje

Eta:

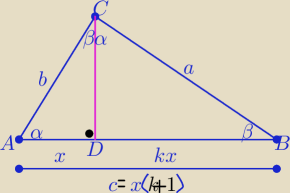
Mila: Według rysunku Ety 1) a+b=m, c=x*(k+1) 2) h²=x²*k, h=x√k Pole Δ na dwa sposoby: ab=c*h⇔ ab=x²√k*(k+1) (a+b)²=m² a²+b²+2ab=m² x²(k+1)²+2*x²√k*(k+1)=m² x²*[(k+1)²+2√k*(k+1)]=m²

	m2
x2=
	(k+1)*(k+1+2√k)

	m2
x2=
	(k+1)*(√k)+1)2

	m		m
|AD|=x=		i kx=		=|DB|
	(√k+1)*√k+1		(√k+1)*√k+1

=======================================