Czworokąt
Matematyk: Wykaż, że w dowolnym czworokącie wypukłym środki jego boków są wierzchołkami pewnego
równoległoboku
28 lut 19:00
edi:
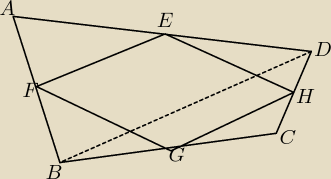
|AE| = |ED|
|DH| = |HC|
|CG| = |GB|
|BF| = |FA|
| | |AF| | | |AE| | |
Zauważamy, że |
| = |
| |
| | |BF| | | |ED| | |
Stąd, na mocy twierdzenia odwrotnego do twierdzenia Talesa FE || BD
| | |CH| | | |CG| | |
Zauważamy, że |
| = |
| |
| | |HD| | | |GB| | |
Stąd, na mocy twierdzenia odwrotnego do twierdzenia Talesa BD || GH
Skoro FE || BD i BD || GH, to FE || GH
Analogicznie postępujemy dla odcinków FG i EH
Czworokąt FEHG ma dwie pary boków równoległych więc jest równoległobokiem, co należało
udowodnić
28 lut 19:23
em: Czy ktoś mógłby rozwiązać to samo zadanie za pomocą wektorów lub dać wskazówkę jak je
rozwiązać?
2 paź 19:26
Vax: | | 1 | | 1 | | 1 | |
FE→ = FA→+AE→ = |
| (BA→+AD→) = |
| (BD→) = |
| (BC→+CD→) = GC→ + CH→ = GH→ |
| | 2 | | 2 | | 2 | |
Analogicznie GF
→ = HE
→ co dowodzi tezy.
2 paź 19:45
em: Dziękuję
3 paź 16:59
 |AE| = |ED|
|DH| = |HC|
|CG| = |GB|
|BF| = |FA|
|AE| = |ED|
|DH| = |HC|
|CG| = |GB|
|BF| = |FA|