wykres - liczby zespolone bluee: Czy ktoś mógłby ocenić czy dobrze myślę....? Narysuj zbiór liczb zespolonych spełniających warunek. a). {z∊C: |z|≥1} Koło o promieniu 1 i środku w początku układu. Zakreskowuję obszar poza nim. b). {z∊C: Im(z)≥Re(z)} Prosta x=y. Zakreskowuję obszar nad nią.

	3
c). {z∊C: π≤Arg(z)≤		π} Dwie proste x=0 oraz y=−x. Zakreskowuję obszar między nimi w II
	2

ćwiartce. d). {z∊C: |z−1|≥3} Koło o promieniu 3 i środku w punkcie 1,0. Zakreskowuję obszar poza nim.

ite: We wszystkich przykładach jest znak większe równe /mniejsze równe/. Uwzględnij to w odpowiedziach. c/ popraw rozwiązanie, sprawdź ćwiartkę układu współrzędnych. Dlaczego x=0 oraz y=−x ?

bluee: C). Y=0 oraz y=x ćwiartka iii Mam jeszcze jedną zagwozdkę... Postać trygonometryczna z liczby z=−3i |z|= √3

	−3
Cos=0 sin=		=−√3
	√3

W odpowiedzi mam z=√3(cos 3pi/2 + i sin 3pi/2)

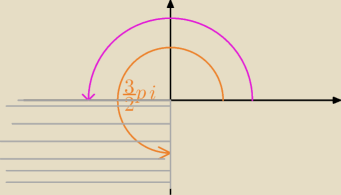
ite: c/ wnętrze kąta z ramionami i wierzchołkiem 18:28 brak oznaczeń kąta po nazwach f. trygonometrycznych powinno być |z|=3

bluee: Tak już się zorientowałam, że |z|=3. Ale i tak nie zgadza się z odpowiedzią. tam z=√3(cos... Dziękuję za pomoc z C

ite: c/ bez wierzchołka ← poprawiam

bluee: Ok W tej odpowiedzi do z=−3i chyba jest błąd

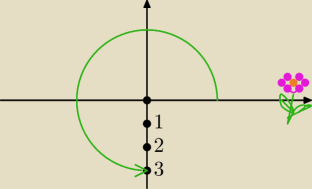
ite: ten pierwiastek się nie zgadza

bluee: Który pierwiastek √0+(−3)²=3

ite: z=√3(cos 3pi/2 + i sin 3pi/2)

bluee: Ok

ite: tak jest zapisane w odpowiedzi?

bluee: TAK

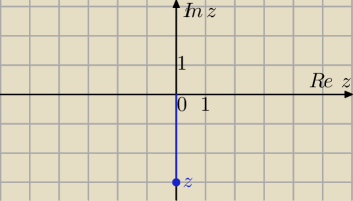
Mila: z=−3i |−3i|=3