funkcje salamandra: Czy obraz zbioru A w odwzorowaniu od f to po prostu "zawężony" zbiór wartości? a) f(x)=x² A=[−1. 1]={x∊R: −1≤x≤1} b) f(x)=sin(x) A=(0;π)={x∊R: 0<x<π} a) f(−1)=1 f(1)=1 Yf=<0;1> b) Yf=(0;1)

salamandra:

	⎧	1 x∊Z
c) f(x)=	⎩	0 x∉Z	A=[0,1]

Yf=<0;1>

	⎧	1 x∊Z
d)f(x)=	⎩	0 x∉Z	A=(0,1)

Yf=(0)

ite: c/ popraw

salamandra: oczywiście Yf=(0,1)

ite: d/ zapis do poprawienia

salamandra: d)Yf={0} c) {0,1}

ite: zbiór wartości funkcji z punktu c/ to {0,1}, więc obraz zbioru A nie może być taki jak podajesz

ite: OK o to chodziło : )

ite: a/ OK b/ do poprawienia

salamandra: A na czym polega przeciwobraz? W kolejnym zadaniu mam wyznaczyć przeciwobraz. a) f(x)=x² A=[1,2]

znak: Przeciwobraz − dostajesz wynik i szukasz argumentów, dla których dostaniesz dany przedział. f⁻¹([1, 2]) = {x ∊ X: f(x) ∊ [1, 2]} Czyli wynik to x ∊ [−√2, −1] ∪ [1, √2]

salamandra: rozumiem, dziękuję

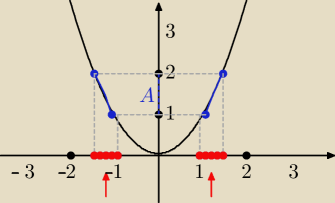
ite: te czerwone przedziały są odpowiedzią

ite: jeszcze popraw b/ z 10:54

salamandra: (0;1>?

ite: Tak jest, nie sugeruj się, jakim przedziałem jest zapis zbioru A, ale jakie wartości w tym przedziale osiąga funkcja.

salamandra: Ok, dzięki. W ogóle, jaka jest różnica między zapisem "[", a "<"? Są one równoważne?

ite: te symbole są używane wymiennie, w średnich szkołach raczej "<"

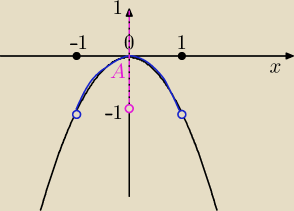
salamandra: b) f(x)=sinx A=0 f⁻¹{0}={x∊X: f(x)=0} x=kπ k∊ℤ c)f(x)=cosx A=(1,2) f⁻¹(1,2)={x∊X: f(x)∊(1;2)} x∊∅ d)f(x)=−x² A=(−1,1) f⁻¹(−1,1)={x∊X: f(x)∊(−1,1)} x∊(−1,0> ok?

ite: b/,c/ przeciwobrazy się zgadzają, w d/ nie

ite:

salamandra: d) x∊(−1;1)?

salamandra: ok, myślałem, że jak wykracza poza zakres (no bo f(x)≠1), to przerywamy w tym momencie, gdzie przekraczamy wartość 0.

Adamm: f|A(B) = f(A∩B)