Funkcja wykładnicza Szkolniak: Witam. Ostatnio na lekcji dostałem zadanie, które brzmiało: ''Wyznacz wartości parametru m, dla których równanie f(x)=m ma dwa pierwiastki różnych znaków''. Funkcja ma postać: f(x)=2^|x+2| Postanowiłem że spróbuję rozwiązać to zadanie algebraicznie, ale coś mi ciągle nie wychodzi i nie mam pojęcia gdzie jest błąd.. Moje rozwiązanie: 2^|x+2|=m, m>0 |x+2|=log₂(m) x+2=log₂(m) v x+2=−log₂(m) x=log₂(m)−2 v x=−log₂(m)−2 Niech x₁=log₂(m)−2 i x₂=−log₂(m)−2, przechodzę teraz do dwóch możliwości: (x₁>0 ∧ x₂<0) v (x₁<0 ∧ x₂>0) (log₂(m)−2>0 ∧ −log₂(m)−2<0) v (log₂(m)−2<0 ∧ −log₂(m)−2>0)

	1		1
(log2(m)>log2(4) ∧ log2(m)>log2(		)) v (log2(m)<log2(4) ∧ log2(m)<log2(		))
	4		4

	1		1
(m>4 ∧ m>		) v (m<4 ∧ m<		)
	4		4

	1
(m>4 v m<		) ∧ m>0
	4

	1
m∊(0;		)∪(4;+∞)
	4

W odpowiedziach jest jedynie przedział (4;+inf) i właśnie nie mam pojęcia co z tym przedziałem

	1
od 0 do		.. W czym tkwi błąd?
	4

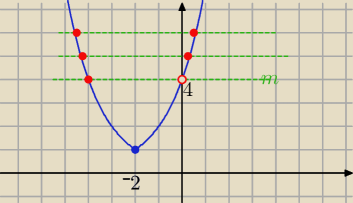
Eta: Graficznie ! |x| T[−2,0] y=2^x → y=2^|x| → y=2^|x+2| m∊(4,∞) ========= i po ptokach

ABC: nie pomyśłał że zbiór wartości to <1,+∞) to od razu powinno mu zapalić lampkę ostrzegawczą ,

	1
jakie		?
	4

Szkolniak: Eta o graficznym sposobie wiem, ale gdybym trafił na takie zadanie na maturze to jakoś wolałbym chyba algebraicznie to zrobić, chociaż nie wiem czy nie idzie się o wiele łatwiej pomylić.. ABC czyli jeśli robimy w sposób algebraiczny, to i tak gdzieś w głowie trzeba to sobie nadal graficznie wyobrażać? czy jak?

a7: log₂m=|x+2| 1.x+2=log₂m dla x>−2 m>0 2.−x−2=log₂m dla x<−2 m>0

	m
1. x=log2(		) dla x>−2
	4

	1
2. x=log		dla x<−2 tutaj mamy x<−2 i dlatego te rozwiązania (punkty przecięcia z m)
	4m

zawsze są po lewej stronie osi OY

	m		m
log2(		)>0 ⇒ log2		>log21 czyli m>4 m∊(4,∞)
	4		4

Eta: Bez logarytmów! dla x≥ −2 y= 4*2⁴ dla x=0 y=4 po wyżej 4 punkty wykresu leżą po prawej stronie

	1
dla x<−2 y=		2−x punkty wykresu leżą po prawej stronie
	4

zatem równanie ma dwa pierwiastki różnych znaków dla m >4

Eta: Poprawiam zapis

	1
dla x<−2 y=		2−x punkty leżą po lewej stronie powyżej y=4
	4