Czy następująca funkcja jest różnowartościowa? Shizzer: f(x) = √x + √x + 2 Oto moje rozwiązanie: Dziedzina funkcja f(x): x ≥ 0 ∧ x + 2 ≥ 0 x ≥ 0 ∧ x ≥ −2 D = x ∊ [0, +∞) Funkcja f(x) jest różnowartościowa, gdy: ∀x₁, x₂ ∊ D : x₁ ≠ x₂ ⇒ f(x₁) ≠ f(x₂) Z prawa kontrapozycji (bo jak dla mnie zapis jest nieco czytelniejszy): ∀x₁, x₂ ∊ D : f(x₁) = f(x₂) ⇒ x₁ = x₂ Przypuśćmy więc, że f(x₁) = f(x₂). Jeśli tak to... √x₁ + √x₁ + 2 = √x₂ + √x₂ + 2, dla x₁, x₂ ∊ D ... x₁ + √x₁ * √(x₁ + 2) = x₂ + √x₂ * √(x₂ + 2) Powinienem dojść do tego, że x₁ = x₂, bo odpowiedzią jest, że funkcja JEST różnowartościowa. Ktoś pomoże mi policzyć to działania z pierwiastkami? Nie mam pomysłu jak to sprowadzić do prawidłowej postaci końcowej

a7: √x₁+√x₁+2=√x₂+√x₂+2 |² po uproszczeniach wychodzi x₁(x₁+1)=x₂(x₂+1) czy to coś pomaga?

a7: oj źle

ABC: jest polecenie "pokaż z definicji" ? jeśli nie, to suma dwóch funkcji rosnących jest rosnąca, a więc różnowartościowa

ite: Tak na przyszłość może się przydać w definicji ∀x₁, x₂ ∊ D : x₁ ≠ x₂ ⇒ f(x₁) ≠ f(x₂) można przekształcić zapis do postaci x₁ − x₂ ≠ 0 ⇒ f(x₁) − f(x₂) ≠ 0 często przy zapisie f(x₁) − f(x₂) często łatwiej jest zobaczyć rozwiązanie.

Saizou : albo jeśli wiesz, że f(x) nie przyjmuje wartości zerowych, to można

	f(x1)
|		| = 1
	f(x2)

Shizzer: Dzięki wszystkim za odpowiedzi. @ABC nie ma polecenia "pokaż z definicji", ale dopiero zaczynam studiować i wydaję mi się, że wszystko muszę pokazywać jakoś tak "formalnie". Myślałem, że nie przejdzie właśnie suma dwóch funkcji rosnących tylko dowód tej implikacji co napisałem w pytaniu. Jeśli mogę używać krótszych i bardziej intuicyjnych zapisów jeśli nie mam polecenia "pokaż z def." to super − będę z tego korzystał.

Shizzer: Mam jeszcze jedno pytanko. Tutaj też chodzi o sprawdzenie czy funkcja jest różnowartościowa. Tym razem funkcja wygląda tak: f(x) = ln²x − lnx Aby wykazać, że funkcja JEST różnowartościowa mogę pokazać, że jest rosnąca w całej swojej dziedzinie bądź malejąca w całej swojej dziedzinie. Niech D będzie dziedziną funkcji f(x). D = x ∊ (0, +∞) Niech x₁ < x₂ oraz x₁, x₂ ∊ D. Kiedy udowodnię, że funkcja f(x) jest rosnąca w całej swojej dziedzinie bądź malejąca w całej swojej dziedzinie to: − gdy f(x)↗ f(x₁) < f(x₂) − gdy f(x)↘ f(x₁) > f(x₂) Sprawdzenie monotoniczności funkcji f(x): t = lnx, t ∊ R g(t) = t² − t = t(t − 1) t₁ = 0, t₂ = 1 p − wierzchołek paraboli p = ¹₂ Zatem funkcja g(t)↗ dla t ∊ [¹₂, +∞) i g(t)↘ dla t ∊ (−∞, ¹₂) Z powyższego wynika, że funkcja f(x) nie jest monotoniczna, a zatem NIE JEST różnowartościowa. Ok jest to rozwiązanie?

ite: Jeśli implikacja p⇒q jest prawdziwa, to z tego nie wynika logicznie, że ¬p⇒¬q też jest prawdziwa. funkcja monotoniczna → f.różnowartościowa ale czy niemonotoniczna → nieróżnowartościowa ?

Shizzer: No tak. Nie przemyślałem tego do końca. W takim razie jak można ruszyć ten przykład?

ite: Funkcja g(t) ma dwa miejsca zerowe. Sprawdź, czy f(x) = ln²(x) − ln(x) również. Jeśli tak, to pokażesz, że nie jest różnowartościowa .

Shizzer: Właściwie to funkcja f(x) = ln²x − lnx jest funkcją kwadratową (chyba, że się mylę) więc nie jest injekcją więc nie jest różnowartościowa. Wystarczyłby taki komentarz czy trzeba to rozpisać?

ite: funkcja kwadratowa ma postać f(x)=ax²+bx+c, gdzie x∊ℛ i a≠0 i a,b,c∊ℛ, więc ta nie jest kwadratowa

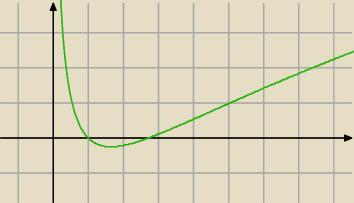
a7: rysunek nie zawadzi

ite: oczywiście zwłaszcza że widać, że nie jest kwadratowa : )

a7: f(x)=0 ln(x)=0 lub ln(x)=1 czyli x=1 lub lnx=lne czyli x=1 lub x=e≈2,7

Shizzer: Powyższy przykład udało mi się zrobić. Mam problem jeszcze z dwoma. 1) f(x) = xarctg2x −> tutaj zupełnie nie wiem jak mam do tego podejść, bo nie widzę, żeby z definicji dało się ten przykład ruszyć, z monotoniczności funkcji też za bardzo nie widzę jak to zrobić. Znaleźć przykład obalający tezę, że ta funkcja jest różnowartościowa też mi ciężko. 2) f(x) = arcsin²x + 2arcsinx −> w tym przykładzie już coś zrobiłem, ale niestety nie wiem czy dobrze. D_f(x) = x ∊ [−1, 1]

	π		π
t = arcsinx, t ∊ [−		,		]
	2		2

g(t) = t² + 2t = t(t + 2) t₁ = 0, t₂ = −2 p = −1 g(t)↗ dla t ∊ [−1, +∞) g(t)↘ dla t ∊ (−∞, −1) Sprawdzam czy funkcja f(x) jest monotoniczna w całej swojej dziedzinie: Proporcja − zamiana radiany na stopnie: 360^o − 2π x − −1

	π
Stąd x ≈ −57o > −
	2

	π		π
Więc g(t)↗ dla t ∊ [−57o,		) i g(t)↘ dla t ∊ (−		, −57o)
	2		2

No i tutaj udowodniłem, że funkcja jest niemonotoniczna. Mogę sprawdzić czy ma 2 miejsca zerowe. t₁ = 0, t₂ = −2

	π		π
arcsinx1 = 0, arcsinx2 = −115o ⊄ [−		,		] ⇒ funkcja f(x) ma jedno miejsce zerowe:
	2		2

x₁ = 0 Podsumowując: Udowodniłem, że funkcja f(x) nie jest monotoniczna i ma jedno miejsce zerowe. I już się trochę w tych moich rozważaniach pogubiłem. Skoro nie zdołałem udowodnić, że funkcja JEST różnowartościowa poprzez badanie jej monotoniczności to straciłem sporą część czasu. Czy to do czego doszedłem na końcu mogę do czegoś wykorzystać i czy droga którą obrałem jest poprawna?

a7: b) ta funkcja nie jest różnwartościowa https://www.wolframalpha.com/input/?i=y%3D+x*arctg2x

a7: to miało być 1)

Shizzer: Dobra, czyli do niektórych przykładów najbardziej pomocny będzie wykres − rozumiem i dziękuję za pomoc. A drugi przykład?

a7: to znaczy wykres jest chyba pomocniczy, że jak widzisz wykres to przynajmniej wiesz jaka jest odpowiedź

a7: 2)tu wychodzi, że jest rosnąca i różnowartościowa https://www.wolframalpha.com/input/?i=y%3Darcsin2x%2B2arcsinx

a7: przepraszam zły input

a7: https://www.wolframalpha.com/input/?i=y%3D%5B%28arcsinx%29%5D%5E2%2B2arcsinx

a7: ta druga funkcja ma zawijas i nie jest różnowartościowa,

Shizzer: Tylko teraz jak do tego dojść bez szkicowania wykresów?

a7: no właśnie nie jestem pewna, ale jeśli funkcja ma punkt minimum to wiadomo, i jest na pewnym odcinku malejąca a potem rosnąca i przy tym jest ciągła to już chyba można wnioskować, że jest różnowartościowa, tak mi się wydaje, lepiej żeby ktoś jeszcze potwierdził

Shizzer: Właśnie! Bo ja opierałem się na tym, że ite wczoraj napisała, że z implikacji monotoniczna ⇒ różnowartościowa nie wynika, że niemonotoniczna ⇒ różnowartościowa, ale ta implikacja nie zachodzi ze względu na to, że istnieją funkcje, które nie są ciągłe. Też mi się wydaję, że jeśli funkcja JEST CIĄGŁA i ma maksimum bądź minimum to NIE JEST funkcją różnowartościową

a7: no to by było fajnie, tylko może jeszcze ite albo ktoś zerknie i potwierdzi