trapez zuza: W trapezie ABCD o podstawach AB i CD przekątne przecinają się w punkcie P Przez punkt P poprowadzono prostą równoległą do podstaw, która przecina ramię AD w punkcie R Wiedząc,że |AB|+|CD|=|AD| Wykaż,ze kąt BRC jest kątem prostym

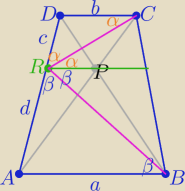
Eta: 1/rysunek... 2/ z tw. Talesa

	c		b
		=		/ +1
	d		a

	c+d		a+b
		=		⇒ d=a bo z treści zadania a+b=c+d
	d		a

to c=b zatem trójkąty RDC i ABR są równoramienne i z własności kątów naprzemianległych mamy: 2α+2β=180^o ⇒ α+β=90^o i mamy tezę |∡CRB|=90^o

a7:

	c		b		c		zielony odcinek
czy na pewno		=		? dlaczego tak? a nie		=
	d		a		d		a

Eta:

c		DP		b
	=		=
d		PB		a

a7: nie rozumiem

a7: ale nic, to Zuza ma rozumieć...

Eta: Jak .......nie rozumiesz?

	c		DP
ΔABD∼ΔDRP ⇒		=
	d		PB

	DP		b
i ΔABP ∼ΔCPD ⇒		=
	PB		a

	c		b
to		=
	d		a

Czy już jasne ?

a7:

	c		DP
no tak, tylko jeszcze nie rozumiem dlaczego można		=		?
	d		PB

a7: aaa to z tw.Talesa?

a7: ok, dzięki

a7:

Eta: