Okres podstawowy berys: Wyznacz okres podstawowy funkcji f(x)=2sin(3x)+3cos(2x)

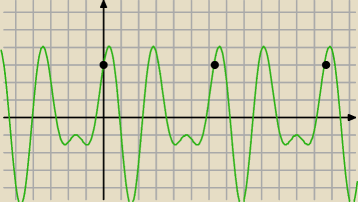
a7: nie znam odpowiedzi, ale rysunek pomocniczy nie zaszkodzi : )

a7: f(x)=2(3sinx−4sin³x)+3(1−2sin²x) f(x)=−8sin³x−6sin²x+6sinx+3 ?

berys: aaa czyli mamy okresowość co 2π bo potęgi i współczynniki przed sinusami nic w aspekcie okresowości nie zmieniają

a7: no właśnie na to wygląda, wypadałoby to rozpisać jakoś że np. suma funkcji o okresie podstawowym T będzie również miała okres podstawowy T

Eta:

	2π
sin(3x) : T=
	3

	2π		4π		6π
T1:		,		,		=2π
	3		3		3

cos(2x) : T= π T₂: π,2π, Okres podstawowy f(x) : T=2π

Mila: Liczyłam dwa razy z definicji, ale gdzieś mam pomyłki, sprawdzam . 2sin(3x)+3cos(2x)=2*sin(3(x+T))+3*cos(2(x+T)), T>0 i T niezależne od x

Mila: Po skorzystaniu ze wzorów na różnicę sinusów oraz różnicę cosinusów, ..

	T
wyłączamy sin(		)
	2

	T
sin(		)=0
	2

T
	=kπ,
2

T=2π