Wyznaczanie zbioru wartości
berys: Jak znaleźć zbiór wartości funkcji 1/(x−x2) ?
Nie wiem co się dzieje w przedziale (0;1)
22 paź 12:05
student: niech x = sin
2t
| 1 | | 1 | | 1 | | 1 | |
| = |
| = |
| = |
| = |
| x−x2 | | sin2t−sin4t | | sin2t(1−sin2t) | | sin2tcos2t | |
Teraz już widzisz?
22 paź 12:11
berys: nie rozumiem co z tego wynika, przekształciłem sobie tę funkcję do postaci 1/x + 1/(1−x) i z
tego
chciałem jakoś naszkicować wykres a następnie zobaczyć jaki jest zbiór wartości ale nie udało
mi się
22 paź 12:18
Adamm:
1/(x−x2) = f(g(x)) gdzie f(y) = 1/y, g(x) = x−x2
wystarczy znaleźć zbiór wartości g(x) w przedziale (0, 1), a potem zbiór wartości
f(y) w tamtym zbiorze wartości poprzednim
22 paź 12:24
Maciess: A tak szkolnie
| 1 | |
| =a /(mnozymy przez mianownik) |
| x−x2 | |
ax
2−ax+1=0
Zastanów się dla jakich a to równanie ma rozwiązanie. Zastanów się osobno co sie dzieje dla a=0
22 paź 12:31
a7:
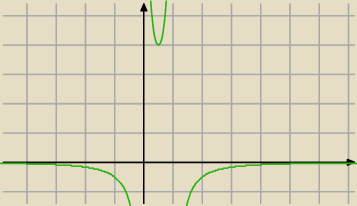
22 paź 12:41
berys: Adamm już rozumiem dzięki, czyli dla a od −∞ do 0 otwartego i od 4 domknięte do nieskończoności
22 paź 12:52
