zespolone hubik: Hej, mam pytanie co do liczb zespolonych Mam takie równanie: x⁴−i=0 No to robię x⁴ = i x1 = −⁴√i x2 = ⁴√−i x3 = −√i x4 = i^3₄ Ale podobno to zła odpowiedź i poprawna jest to ⁸√−1, stąd pytanie. Dlaczego? XD

ICSP: ⁸√−1 ma 8 elementów kiedy x⁴ − i = 0 ma tylko 4 rozwiązania.

hubik: No tak, tylko dlaczego ma być 8 a nie 4?

ICSP: ma być 4.

hubik: Czyli moja odpowiedź jest dobra? XDD

ABC: jeśli coś jest rozwiązaniem równania x⁴=i to jest rozwiązaniem równania x⁸=−1 , ale odwrotnie być nie musi

Mila: x⁴−i=0⇔

	2i
x4=
	2

	(1+i)2
x4=		⇔
	2

	1+i		1+i
x2=		lub x2=−
	√2		√2

	1+i		−(1+i)
x2=√2*		lub x2=√2*
	2		2

	√2		√2		√2		√2
x2=		+i*		lub x2=i2*(		+i*		)
	2		2		2		2

rozwiązuj dalej sam

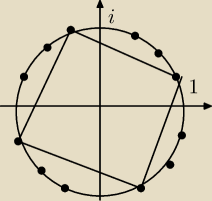
jc: Rozwiązania równania x⁴=i leżą w wierzchołkach kwadratu. punkt w pierwszej ćwiartce = cos π/8 + i sin π/8 pozostałe rozwiązania uzyskasz mnożą rozwiązanie z pierwszej ćwiartki przez i, −1, −i.

	1+cos 2a
cos2 a =
	2

	1− cos 2a
sin2 a =
	2

cos π/8 = √ (1 + 1/√2)/2 sin π/8 = √ (1 − 1/√2)/2