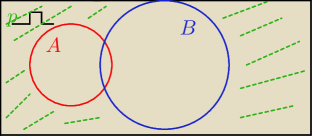
zbiory salamandra: Wykaż, że dla dowolnych zbiorów A i B a) (A ∪ B)' = A' ∩ B' b) (A ∩ B)' = A' ∪ B' czy można wykazać za pomocą takiego rysunku i odpowiednio podpisując? W tym wypadku zrobiłem przykład a), no i (A∪B)' to wszystko na zewnątrz, A' to wszystko oprócz A, B' to wszystko oprócz B, a część wspólna z tego, to zostanie właśnie to co na zewnątrz, bo wykluczymy w A' zbiór B, a B' zbiór A. To jedyny sposób jaki mi świta jeszcze za czasów matury, nie wiem, czy tutaj wymagają czegoś innego?

ICSP: Rysunek to nie dowód

ICSP: Wpisz w google prawa de Morgana dowód. Powinno coś wyskoczyć.

salamandra: No to jeśli tak jak zrobiłem nie można, to na ten wieczór się poddaję. Mimo to dzięki za wskazówkę, jutro przed zajęciami może zdążę to ogarnąć.

an: Tablica prawdy coś słyszałeś

Eta: x∊(AUB)^'⇔ x∉(AUB)⇔ ∼[x∊(AUB)]⇔∼[x∊ A v x∊B]⇔x∊A^' ∧ x∊B^'⇔ x∊(A^'∩B^')

Eta: Drugie prawo analogicznie .....