zbiory
salamandra: Dane są zbiory: A = {x ∈ R : −2 ≤ x ≤ 2}, B = {x ∈ R : 0 ≤
x ≤ 1}, C = {x ∈ Z : −3 < x < 5}. Narysuj zbiory:
a) A × B
b) A × C
c) (A \ B) × B
d) (A × B) \ (B × B)
Nie bardzo wiem jak to narysować, gdy nie ma "y", więc nie będzie to prostokąt?
18 paź 23:37
znak: O ile dobrze pamiętam, to oznaczenie nie ma znaczenia. Można te zbiory "przekształcić":
A = {x ∊ R: −2 ≤ 2 ≤ 2} = <−2, 2>
B = <0, 1>
C = (−3, 5)
18 paź 23:40
salamandra: To to ja wiem, ale nie wiem w tym momencie jak narysować iloczyn kartezjański, gdyż w trzech z
tych zbiorów jest mowa o współrzędnej x, a w żadnej o "y", a we wprowadzeniu przed zadaniami
nie jest pokazany taki przypadek.
18 paź 23:42
wredulus_pospolitus:
'x' <−−− iloczyn kartezjański
W praktyce
A x B = <−2 ; 2> x <0 ; 1> czyli prostokąt (wraz z brzegami) o x ∊<;2 ; 2> i y∊<0;1>
18 paź 23:44
wredulus_pospolitus:
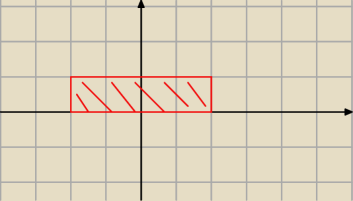
18 paź 23:45
salamandra: Aha, myślałem, że jak w B nie ma y∊R, to nie traktujemy tego jak prostokąt
18 paź 23:46
wredulus_pospolitus:
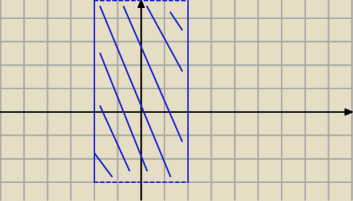
18 paź 23:46
znak: To nie ma znaczenia, że tam nie ma "y". Mogłoby być równie dobrze "k".
18 paź 23:47
salamandra: Zmyliło mnie to, bo nad zadaniami mam dwa przykłady i w obu w zbiorze B jest y∊R
18 paź 23:47
wredulus_pospolitus:
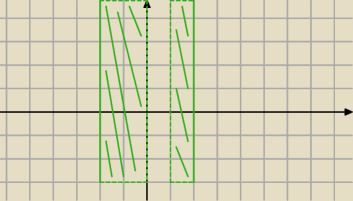
przerywane: y = 5 i y = −3 oraz x = 0 i x = 1
nieprzerywane: x = −2 i x=2
18 paź 23:49
znak: Rozumiem, tak to już z tymi przykładami jest. Generalnie nie ma to znaczenia.
18 paź 23:49
wredulus_pospolitus:
Salamandra ... oznaczenia ... to wszystko kwestia oznaczeń ... istotne jest by wiedzieć, że w A
x B pierwszy zbiór to pierwsza współrzedna punktu (x'sy), drugi zbiór to druga współrzedna
punktu (y'reki)
18 paź 23:50
salamandra: Teraz już jasne, dzięki

, rozumiem, że jak dany obszar już nie wchodzi w skład iloczynu, to
zaznaczamy fragment na prostokącie przerywaną linią?
18 paź 23:54
salamandra: Jaki zrobiłeś przykład 23:49? Bo coś mi się nie zgadza
18 paź 23:55
wredulus_pospolitus:
(A\B) = <−2 ; 0) u (1 ; 2>
18 paź 23:57
wredulus_pospolitus:
aaa ... tam jest 'x B' jak zrobiłem 'x C'

18 paź 23:58
wredulus_pospolitus: no to popraw moje " po y'reku "
18 paź 23:58
salamandra: no mam po y'reku <0;1>
w d) mam x∊<−2;0) U (1;2>, a y∊<0;1>
19 paź 00:01
wredulus_pospolitus:

19 paź 00:12


 przerywane: y = 5 i y = −3 oraz x = 0 i x = 1
nieprzerywane: x = −2 i x=2
przerywane: y = 5 i y = −3 oraz x = 0 i x = 1
nieprzerywane: x = −2 i x=2
 , rozumiem, że jak dany obszar już nie wchodzi w skład iloczynu, to
zaznaczamy fragment na prostokącie przerywaną linią?
, rozumiem, że jak dany obszar już nie wchodzi w skład iloczynu, to
zaznaczamy fragment na prostokącie przerywaną linią?

