ostrosłup mat20: Dany jest ostrosłup prawidłowy trójkątny w którym krawędź podstawy jest trzy razy krótsza od krawędzi bocznej. Promień okręgu wpisanego w podstawę ma długość r Wyznacz pole przekroju tego ostrosłupa płaszczyzną prostopadłą do krawędzi bocznej i przechodzącą przez krawędź podstawy. Sporządź odpowiedni rysunek.

wredulus_pospolitus: Rysunek sporządziłeś? Zaznaczyłeś przekrój o który chodzi? Wyznaczyłeś ile wynosi długość krawędzi podstawy? A ile krawędź boczna? Zrobiłeś cokolwiek

Eta: Hej "Wredny" Coś taki ostry ?

wredulus_pospolitus: Taki jak zawsze ... no może troszeczkę bardziej, bo się dzisiaj wyspałem

Eta: ........ robaczywe

wredulus_pospolitus: supcio ... trochę bonusowego białka Zresztą −−− gdzie Ty (w dzisiejszych czasach) dopadłaś robaczywe jabłko? Toż to jakiś 'bio rarytas'

Eta: Z mojego sadu ( nie opryskiwane)

Eta: No może przez mojego

Eta:

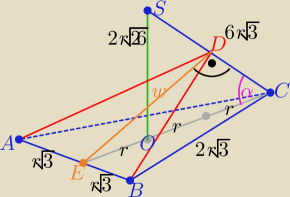
	√26
W ΔCOS : z Pitagorasa H=2√26 to sinα=
	3√3

w ΔDEC : w= 3r*sinα = ....

	1
P(ABD)=		*|AB|*w=r√3*w
	2

P= r²√26 =========== i po ptokach

ICSP: Zadania z stereometrii i planimetrii to najgorsze zło tego świata.

Eta: Najlepsze co może być !

wredulus_pospolitus: Etuś ... najlepsze są z prawdopodobieństwa

Eta: Poprawiam zapis H=2√26 r

Eta: Etammmmmmmm ... "sztampowe, oklepane,.....