Interpretacja geometryczna modułu liczb zespolonych Student: Korzystając z interpretacji geometrycznej modułu liczb zespolonych obliczyć, dla jakich liczb zespolonych z, |z| ≤ 1 wyrażenie |2−3i−z| przyjmuje wartość największą i najmniejszą. Proszę o pomoc.... Rozumiem, że mam to zrobić z "okręgu", ale nie wychodzi mi. Jak prawidłowo poradzić sobie z minusem przy z?

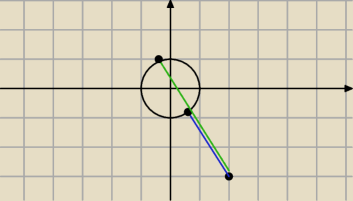
luui: f(z) = |z − ( 2−3i)| , |z| ≤ 1 f_min : IV ćwiartka (x>0 i y<0)

	2−3i
dla z1 =		rzut szukanego wektora o module = 1 w kierunku wektora [2, −3]
	√13

f_max : II ćwiartka (x<0 i y>0)

	−2+3i
dla z2 =
	√13