Funkcja homograficzna Daniel: Dana jest funkcja homograficzna: f(x) = 2 + a/x−3 gdzie a > 0 oraz x > 3. Na wykresie tej funkcji wybrano dowolny punkt P. Uzasadnij, że pole prostokąta, którego przeciwległymi wierzchołkami są punkt P oraz punkt przecięcia się asymptot funkcji ƒ(x), nie zależy od wyboru punktu P.

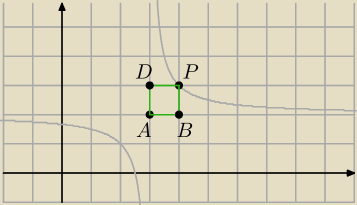
a7: a=1 A=(3,2) P=(x,y) B=(x,2) D=(3,y) Pole_ABPD=1²=1 |AB|=√(x−3)²+0²=x−3 |BP|=|AD|=√(3−3)²+(y−2)²=y−2

	1		2x−6+1		2x−5
y=2+		=		=
	x−3		x−3		x−3

	2x−5
POLEABPD=|AB|*|AD|=|AB|*|BP|=(x−3)*(y−2)=(x−3)*(		−2)=1 c.n.u.
	x−3

a7: w ogólności y=2+{a}{x−3} asymptota pozioma y=2 , asymptota pionowa x=3 A=(3,2) P=(x,y) B=(x,2) D=(3,y) |AB|=jak w poprzednim poście=x−3 |BP|=|AD|=y−2

	a		a
y=2+		y−2=
	x−3		x−3

	a
POLEABPD=|AB|*|AD|=|AB|*|BP|=(x−3)*(y−2)=(x−3)*		=a c.n.u.
	x−3

Eta:

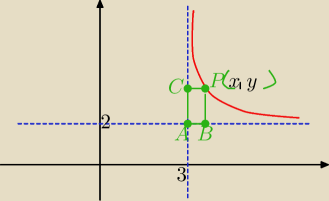
	a
|AB|= x−3 , x>3 |AC|= y−2 i y−2=		, a>0
	x−3

P=(x−3)(y−2)= a −−pole nie jest zależne od wyboru punktu P