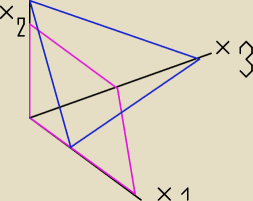
Wyznacz część wspólną obszarów (3 wymiary) ZGoryDziekuje: Hej, chciałabym rozwiązać graficznie nierówności z 3 niewiadomymi, tak, aby funkcja f była zmaksymalizowana. Dana funkcja to f(x₁,x₂,x₃)=12x₁+18x₂+12x₃. Ale chyba nie ma to znaczenia, zwracają uwagę na to, o co chcę zapytać. Kolorami wyznaczone linie mają tworzyć (chyba)płaszczyzny Płaszczyznę różową wyznaczyłam z nierówności: 1,5x₁+3x₂+4x₃≤1500 A płaszczyznę niebieską z nierówności: 3x₁+2x₂+x₃≤1200 Mam problem z wyznaczeniem części wspólnej tych dwóch płaszczyzn. Ile ta płaszczyzna będzie miała wierzchołków? Jak wyznaczyć ich współrzędne? Podane nierówności oraz funkcja wynikają z treści zadania. Czy istnieje jakiś ogólnodostępny program, który zaznaczy podane ograniczenia na wykresie? Przepraszam za chaos, ale treść zadania wynika z jego ekonomicznej interpretacji.

ZGoryDziekuje: Kolejnymi x−ami chciałam oznaczyć odpowiednie osie. Rysunek oczywiście wykonałam na kartce papieru. Tu mam problem z jego pokazaniem.

jc: f(x,y,z)=6(2x+3y+2z) 3x+6y+8z ≤ 3000, niektórzy nie lubią ułamków 3x+2y+z ≤ 1200 x=−10t y=21t z=−12t t ≥ 0 x, y, z spełniają nierówność f(x,y,z)=114t może być dowolnie duże!

ICSP: Jeśli mnie pamięć nie myli to przecięcie dwóch płaszczyzn jest prostą.

jc: Pewnie zgubiły się jakieś nierówności...

ZGoryDziekuje: Każda nierówność odpowiada za płaszczyznę, pierwsza za różową, a druga za niebieską. Ich przecięcie spowoduje powstanie bryły, ale nie umiem jej sobie wyobrazić, ani zaznaczyć. Więcej warunków w zadaniu nie ma.

jc: Dwie płaszczyzny są równoległe lub przecinają się wzdłuż prostej. W tym drugim przypadku dzielą przestrzeń na 4 kliny. Czy na pewno nie było mowy o innych ograniczeniach?

ZGoryDziekuje: x₁,x₂,x₃ są ≥0

ZGoryDziekuje: Więc zapomniałam dodać, że rozpatrujemy przestrzeń dla dodatnich x₁,x₂,x₃.

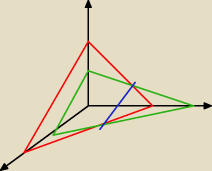
jc: No to teraz masz 5 płaszczyzn.

x		y		z
	+		+		≤ 1, niektórzy nie lubią ułamków
1000		500		325

x		y		z
	+		+		≤ 1
400		600		1200

płaszczyzny przecinają osie y=z, x=z, x=y odpowiednio w punktach: (1000,0,0), (0,500,0), (0,0,350) (400,0,0), (0,600,0), (0,0,1200) (0,0,), (400,0,0), (0,500,0), (0,0,350) Poszukaj dwóch dodatkowych wierzchołków (końców niebieskiego odcinka).

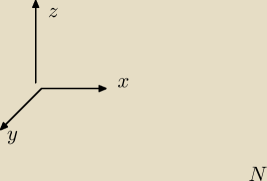
jc: Nie opisałem osi. Mam być tak, jak na drugim rysunku. y=0 3x+8z = 3000 3x+z = 1200 x=? z=? z=0 3x+6y = 3000 3x+2y = 1200 x=? y=?

ZGoryDziekuje: Jeden koniec (ten położony niżej) to w przybliżeniu (314,29 ; 0 ; 257,14)?

ZGoryDziekuje: Przepraszam, rysowałam trochę inaczej, ale wyszły mi wierzchołki (314,29 ; 0 ; 257,14) oraz (100 ; 450 ; 0)

jc: Sprawdź, mogłem coś pomylić. Teraz wystarczy sprawdzić wartości funkcji w wierzchołkach. To zadanie z programowania linowego. Na pewno na jakieś stronie www można wpisać dane i otrzymać odpowiedź.

ZGoryDziekuje: Jest poprawnie Maksymalna wartość funkcji jest osiągana w wierzchołku F i wynosi 9300. Łatwiej chyba rozwiązać to zadanie z użyciem programu dualnego. Prosząc o metodę graficzną przy 3 zmiennych decyzyjnych profesor chciał chyba dostarczyć nam rozrywki Dziękuję za bezcenną pomoc!