Trójkąt prostokątny. Znajdź sinus Jabur: Promień okręgu opisanego na trójkącie prostokatnym jest 2.5raza większy od promienia wpisanego w ten trójkąt. Podaj sinus większego kąta. Proszę o pomoc

kerajs: Taka zależność jest w trójkącie egipskim.

wredulus_pospolitus: a −−− przyprostokątna b −−− druga przyprostokątna r −−− promień okręgu wpisanego R = 2.5r −−− promień okręgu opisanego c = 2R = 5r −−− przeciwprostokątna a = x + r b = 5r − x + r = 6r − x a² + b² = c² x² + 2xr + r² + 36r² − 12xr + x² = 25r² 2x² − 10xr + 12r² = 0 x² − 5xr + 6r² = 0 (x−3r)(x−2r) = 0 −−−> x = 3r lub x=2r stąd: a = 4r ; b = 3r ; c = 5r lub a = 3r ; b = 4r ; c = 5r (czyli ten sam trójkąt) Więc jak widzisz −−− trójkąt egipski

gamma: Warunki zadania spełnia każdy trójkąt prostokątny, którego długości boków zostają w stosunku 3:4:5 (np. trójkąt o bokach długości 1, 4/3, 5/3), a nie tylko trójkąt egipski, którego boki maja długość 3, 4, 5. https://matfiz24.pl/twierdzenie-pitagorasa/trojkat-pitagorejski-i-egipski

wredulus_pospolitus: @gamma ... nikt nie napisał, że TYLKO trójkąt egipski spełnia te warunki

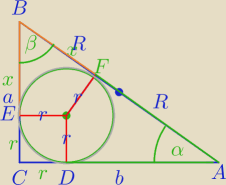
Mila: b>a |BC|=a, |AC|=b R=2.5r 1) |AF|=2R−x=|AD| b=r+2R−x=r+5r−x=6r−x a=r+x 2) Z tw. Pitagorasa: (r+x)²+(6r−x)²=(5r)² x=3r ⋁ x=2r a=r+3r=4r b=6r−3r=3r c=5r

	4
sinα=
	5

	3
sinβ=
	5

α>β lub a=r+2r=3r b=4r c=5r β>α ( jak na rysunku) Δ przystający do poprzedniego

Mila: To samo co u Wredulusa, pisałam na raty i nie spojrzałam, że już jest rozwiązanie. Są też inne sposoby.

Mila: Inny sposób c=2R=5r 1) a+b=2r+2R⇔a+b=7r a+b=7r /² a²+b²+2ab=49r² 25r²+2ab=49r² ab=12r² 2) a=7r−b (7r−b)*b=12r² b²−7rb+12r²=0 Δ=49r²−48r²=r²

	7r−r
b=		=3r lub b=4r
	2

a=4r lub a=3r ============= i liczysz sinusy.

Eta: Dokładnie taki sposób miałam pisać Pozdrawiam Mila .... ( zdrowa?

Eta: Tylko bez delty ab=12r² i a+b= 7r to a=4r i b=3r lub a=3r i b= 4r

Mila: Zdrowa, ale zmęczona ograniczeniami dotyczącymi towarzyskiego życia Siedzimy w domu, ale nawet dla takich domatorów jak my, teraz to już przesada.

Mila: Pozdrawiam

getin: b<a<c − boki trójkąta

	1
R =		c
	2

r = {a+b−c}{2}

	5
R = 2,5r =		r
	2

	a		b
(		)2+(		)2=1
	c		c

	a
sinα =		= ?
	c

	5
R =		r
	2

1		5
	c =		r
2		2

1		5		a+b−c
	c =		*
2		2		2

2c = 5(a+b−c)

	a		b
5		+5		= 7
	c		c

	a		b
{ (		)2+(		)2=1
	c		c

	a		b
{ 5		+5		=7
	c		c

a		b
	= x,		= y oraz x>y
c		c

{ x²+y²=1

	7−5x
{ 5x+5y=7 → y=
	5

	7−5x
x2+(		)2 = 1
	5

	49−70x+25x2
x2+		= 1
	25

25x²+49−70x+25x²=25 50x²−70x+24 = 0 25x²−35x+12 = 0 Δ = 1225−4*25*12 = 25 √Δ = 5

	35−5		3		7−5*35		4
x1 =		=		, y1 =		=		(nie spełnia założenia x>y)
	50		5		5		5

	35+5		4		7−5*45		3
x2 =		=		, y2 =		=		(spełnia założenie)
	50		5		5		5

	4		a		4		4
x =		→		=		→ sinα =
	5		c		5		5

Eta: Może ktoś poda jeszcze dłuuuuuuuuuuuuuuuuższy sposób