przedstawienie graficzne postaci jaros: Cześć wszystkim, wytłumaczył by mi ktoś, jak rozwiązywać przykłady z liczb zespolonych gdzie "arg" i moduł są na siebie nałożone?

	π
|argz| <
	6

a7: a może chodzi zwyczajnie (nie znam się)

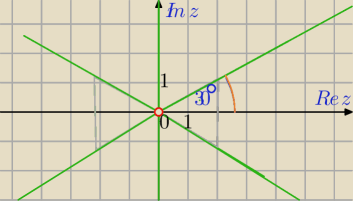
	π		π
−		<argz<
	6		6

jaros: Hmmm ja też nie pomogę, bo wyniku nie mam jedynie wolfram coś dziwnego pokazuje

a7: a jaka jest treść zadania? i co pokazuje wolfram?

jaros: Zaznaczyc na p laszczyznie zbior punktow odpowiadajacy liczbom zespolonym spe lniajacym warunki: https://imgur.com/Kukknju

a7: ta dam .... (?) jest to punkt (dobrze?) https://www.wolframalpha.com/input/?i=z%3D%7Cz%7C*%28cos%7Cpi%2F6%7C%29%2Bisinsin%7Cpi%2F6%7C%29

jaros: Niestety tego nie wiem, nie mam odpowiedzi do zestawu. Pokazała byś mi jak do tego dojść?

a7: nie no wpisałam po prostu do postaci trygonometrycznej liczby z fi φ=|π/6|, ale widzę, że to jeszcze nie to, bo |φ| ma być mniejsza niż π/6

a7: gdy w wolfram wpisuję z=|z|(cosφ+isinφ) & |φ|<(π/6) to Wolram wurzuca fałsz....

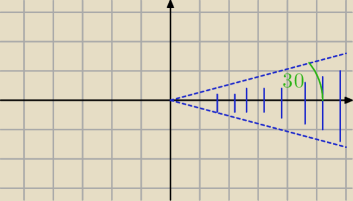luui: arg(z) = α

−π		π
	< α <
6		6

Ograniczenie występuje tylko na argumencie, więc nie ma co się zastanawiać tylko rysować

jaros: O? Ciekawe, naprawdę tylko tyle?

jaros: Znaczy @a7 już to pisała wcześniej ale nie jestem pewny by było to aż takie proste hah. Dziękuję za odpowiedz a jeślii mogę jeszcze spytać, to co w wypadku

	3
0 ≤ arg((1+i)z) <		π
	4

a7: ooo

luui: Przyda się znajomość: arg(z₁z₂) = arg(z₁) + arg(z₂) + 2kπ , k∊Z Spróbuj wyznaczyć arg(1+i) i podstaw do powyższego wzoru, przyjmując k=0 bo interesuje nas 0 ≤ α < 2π

jaros: Niestety nie wiem jak wyznaczać argument z (x+iy+1)

luui: Przeczytaj jeszcze raz wpis z 23:23 arg((1+i)z) = arg(1+i) + arg(z) Wyznaczyć musisz: arg(1+i) = φ Dzięki czemu, będziesz mógł zapisać

	3
0 ≤ φ + arg(z) ≤		π
	4

	3
0 − φ ≤ arg(z) ≤		π − φ
	4

jaros: A to tak można? jak potem zdefiniować "0 − φ "

luui: A no można Oto dowód: https://pl.wikipedia.org/wiki/Liczby_zespolone#Mno%C5%BCenie 0 − φ to przecież różnica kątów (w radianach)

Mila:

	π
v=(1,1), φ=
	4

	3
0≤arg(1+i)+arg(z)+2kπ<		π, k∊Z
	4

	π		3		π
0≤		+arg(z)≤		π /−
	4		4		4

	π		π
−		≤arg(z)≤
	4		2

Zaznaczyć już umiesz?

Landryna: @Mila a mam pytanie co do rozwiązania przykładu z godziny 17:42. W jaki sposób zamieniliśmy

	π
art(1+i) na		bo nie wiem jak to ma się niby zamieniać na radiany
	4

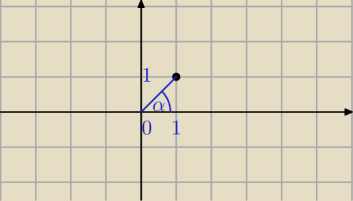Mila: 1) v=1+i co odpowiada na płaszczyźnie punktowi (1,1)

	π
α=45o=
	4

albo 2) |1+i|=√2

	1		√2
cosα=		=
	√2		2

	√2
sinα=
	2

	π
α=
	4

Landryna: O dziękuje ślicznie Super wytłumaczone. A gdybym jeszcze mogła spytać, bo jesteśmy w temacie: arg(z⁶) = π W jaki sposób coś takiego jest rozwiązywalne? argument do 6 potęgi jest równy 180 stopi lub 3,14

Mila: Żadne (3,14), tylko π albo 180^o. arg(z⁶) = π

	π
arg(z)=
	6

z=|z|(cosα+isinα) z⁶=|z|⁶*(cos(6α)+i sin (6α)) czyli: 6α=π

	π
α=
	6

=====]

Landryna: @Mila Ogromne serce Dla PANI<3

Mila: Oj, zapomniałam dodać 2kπ 6α=π+2kπ i warunek na argument. arg(zⁿ)=n arg(z)+2kπ dla pewnego k∊Z 0≤ arg(z)<2π Teraz sama wyznacz arg(z).

Landryna:

	π
Czyli coś takiego? 0 ≤		+ {kπ}{3} ≤ 2π?
	6

Mila:

ICSP: arg(zⁿ) = n*arg(z) (mod [ 0 ; 2π)) Natomiast zapis : 0 ≤ Arg(z) < 2π Powinien mieć już Arg z dużej litery wszak jest to argument główny. Pozostaje wybrać takie k dla których argument wpada w zakres argumentu głównego.

Landryna: Czyli k = 0 tak? jednak troszkę zagmatwany ten przykład, hmm było jasno i logicznie do momentu w 21;38 hahah

ICSP: takie k dla których <− liczba mnoga.

Landryna: sekundę, bo się pogubiłam, to k ∊ (0,2) , Przepraszam, jak napisałam głupotę ale nie rozumiem zbytnio co Pan ma na myśli, że ten argument gdzie nie ma k ma wpadać do niego jakieś k w obrębie (0,2π)

ICSP: spójrz na swój wpis z 22:24 i wybierz wszystkie całkowite k dla których prawdziwe są tamte nierówności.

Landryna: No to już wiem dla k ∊ {0,1,2,3,4,5}, i w jaki sposób przedstawić to na rysunku?

ICSP: dla k = 0 rozwiązaniem jest każda liczba w postaci z = |z|e^iπ/6 czyli jest to półprosta zaczepiona w punkcie (0,0) (bez tego punktu) nachylona od osi

	π
rzeczywistej pod kątem		.
	6

Ostateczny rysunek powinien zawierać 6 takich półprostych.

Landryna: 6 prostych z różnymi kątami, które obliczamy podstawiając 6 liczb naturalnych k?

ICSP: tak. Podstawiając naturalne k dostajesz kolejne kąty. i nie prostych tylko półprostych (kończą się z jednej strony)

Landryna: Dobrze, dziękuje ślicznie już rozumiem

Mila: